SICP第一章习题解答
by wqpw
使用Racket并安装sicp包.
1.8
(define (开立方术 天)
(define (改之 地)
(/ (+ (/ 天 (* 地 地)) (* 2 地)) 3))
(define (可否 地)
(= (改之 地) 地))
(define (迭代 地)
(if (可否 地)
地
(迭代 (改之 地))))
(迭代 1.0))
(开立方术 2)
1.11
#lang sicp
(define (f n)
(if (< n 3)
n
(+ (f (- n 1)) (* 2 (f (- n 2))) (* 3 (f (- n 3))))))
(define (ff n)
(define (f-iter i j k cnt)
(if (< cnt n)
(f-iter (+ i (* 2 j) (* 3 k)) i j (+ 1 cnt))
i))
(if (< n 3)
n
(f-iter 2 1 0 2)))
(define (test n)
(define (test-iter cnt)
(display (cons (f cnt) (ff cnt)))
(if (< cnt n)
(test-iter (+ 1 cnt))))
(test-iter 1))
(test 8)
一个好看的答案:
(define (fi n)
(define (f-iter a b c count)
(cond ((< count 0) count)
((= count 0) a)
((= count 1) b)
((= count 2) c)
(else (f-iter b c (+ c (* 2 b) (* 3 a)) (- count 1)))))
(f-iter 0 1 2 n))
1.12
#lang sicp
(define (贾宪三角 n)
(define (loop i)
(display (增乘法 i (- (+ 1 n) i)))
(display " ")
(if (< i n)
(loop (+ i 1))))
(loop 1))
(define (增乘法 行 列)
(if (or (= 1 行) (= 1 列))
1
(+ (增乘法 (- 行 1) 列) (增乘法 行 (- 列 1)))))
((lambda (n)
(define (loop i)
(贾宪三角 i)
(display "\n")
(if (< i n)
(loop (+ i 1))))
(loop 1)) 8)
1.16
#lang sicp
(define (square n) (* n n))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1))))))
(define (fast-expt-iter b n)
(define (iter a b n)
(if(> n 0)
(if(not (even? n))
(iter (* a b) (square b) (floor (/ n 2)))
(iter a (square b) (floor (/ n 2))))
a))
(iter 1 b n))
(fast-expt 3 9)
(fast-expt-iter 3 9)
其实是照着这个程序改的.
typedef long long ll;
ll mod_pow(ll x, ll n, ll mod) {
ll res = 1;
while (n > 0) {
if (n & 1) res = res * x % mod;
x = x * x % mod;
n >>= 1;
}
return res;
}
(define (iter-fast-expt b n)
(define (iter N B A)
(cond ((= 0 N) A)
((even? N) (iter (/ N 2) (square B) A))
(else (iter (- N 1) B (* B A)))))
(iter n b 1))
1.17和1.18
(define (mul a b)
(if (= b 0)
0
(+ a (mul a (- b 1)))))
(define (double x) (* x 2))
(define (halve x) (floor (/ x 2)))
(define (fast-mul a b)
(cond ((= b 1) a)
((even? b) (fast-mul (double a) (halve b)))
(else (+ a (fast-mul a (- b 1))))))
(define (fast-mul-iter a b)
(define (iter r b)
(if(not (= b 1))
(if(even? b)
(iter (double r) (halve b))
(+ a (iter (double r) (halve b))))
r))
(iter a b))
(mul 5 8)
(fast-mul 5 8)
(fast-mul-iter 5 8)
1.19
由$\begin{cases}a_1=b_0q+a_0q+a_0p\\b_1=b_0p+a_0q\end{cases}$, 带入$\begin{cases}a_2=b_1q+a_1q+a_1p\\b_2=b_1p+a_1q\end{cases}$后计算可得$\begin{cases}a_2=b_0q’+a_0q’+a_0p’\\b_2=b_0p’+a_0q’\end{cases}$, 其中$\begin{cases}p’=p^2+q^2\\q’=2pq+q^2\end{cases}$.
#lang sicp
(define (fib n)
(fib-iter 1 0 0 1 n))
(define (fib-iter a b p q count)
(cond ((= count 0) b)
((even? count)
(fib-iter a
b
(+ (* p p) (* q q))
(+ (* 2 p q) (* q q))
(/ count 2)))
(else (fib-iter (+ (* b p) (* a q) (* a p))
(+ (* b p) (* a q))
p
q
(- count 1)))))
1.22
(define (square x) (* x x))
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
(= (remainder b a) 0))
(define (prime? n)
(= n (smallest-divisor n)))
(define (timed-prime-test n)
(start-prime-test n (runtime)))
(define (start-prime-test n start-time)
(if (prime? n)
(report-prime n (- (runtime) start-time))))
(define (report-prime n elapsed-time)
(newline)
(display n)
(display " *** ")
(display elapsed-time))
(define (search-for-primes n ed)
(define (search st)
(timed-prime-test st)
(if (< st ed)
(search (+ st 2))))
(if (even? n)
(search (+ n 1))
(search n)))
(search-for-primes 10000 10100)
1.23
(define (find-divisor n test-divisor)
(define (next n)
(if (= n 2) 3 (+ n 2)))
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (next test-divisor)))))
1.27
(define (is-carmichael n)
(define (iter i)
(if (< i n)
(if (= (expmod i n n))
(iter (+ i 1))
#f)
#t))
(if (> n 1)
(iter 1)
#f))
(prime? 1105) ;#f
(fast-prime? 1105 100) ;#t
(smallest-divisor 1105) ;5
(is-carmichael 1105) ;#t
(prime? 6601) ;#f
(fast-prime? 6601 100) ;#t
(smallest-divisor 6601) ;7
(is-carmichael 6601) ;#t
1.28
(define (expmod-28 base exp m)
(cond ((= exp 0) 1)
((= 1 (remainder (square base) exp)) 0)
((even? exp)
(remainder (square (expmod-28 base (/ exp 2) m))
m))
(else
(remainder (* base (expmod-28 base (- exp 1) m))
m))))
(define (fermat-test-28 n)
(define (try-it a)
(= (expmod-28 a n n) a))
(try-it (+ 1 (random (- n 1)))))
(define (fast-prime-28? n times)
(cond ((= times 0) true)
((fermat-test-28 n) (fast-prime-28? n (- times 1)))
(else false)))
(fast-prime? 561 100)
(fast-prime-28? 561 100)
(prime? 561)
(fast-prime? 2465 100)
(fast-prime-28? 2465 100)
(prime? 2465)
(fast-prime? 2821 100)
(fast-prime-28? 2821 100)
(prime? 2821)
(fast-prime? 6601 100)
(fast-prime-28? 6601 100)
(prime? 6601)
1.29
from itertools import cycle
def f(x):
return x**3
def xps(f, a, b, n):
assert n%2==0 and n >= 100
h = (b-a)/n
res = 0
def y_k(k):
return f(a+k*h)
co = cycle([4,2])
res += y_k(0)
for i in range(1, n):
res += next(co)*y_k(i)
res += y_k(n)
res *= h/3
return res
print(xps(f, 0, 1, 1000))
#lang sicp
(define (cube x) (* x x x))
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (xps1 f a b n)
(let ((h (/ (- b a) n)))
(define (y_k k) (f (+ a (* k h))))
(define (co c) (if (= c 2) 4 2))
(define (iter i c res)
(if (< i n)
(iter (+ i 1) (co c) (+ res (* c (y_k i))))
res))
(* (/ h 3.0) (+ (y_k 0) (iter 1 4 0) (y_k n)))))
(define (xps2 f a b n)
(define h (/ (- b a) n))
(define (y_k k) (f (+ a (* k h))))
(define (co i)
(cond ((or (= i 0) (= i n)) 1)
((even? i) 2)
(else 4)))
(define (xps-term i) (* (co i) (y_k i)))
(* (/ h 3.0) (sum xps-term 0 inc n)))
(xps1 cube 0 1 1000)
(integral cube 0 1 .001)
(xps2 cube 0 1 1000)
1.30
(define (sum-iter term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (+ result (term a)))))
(iter a 0))
1.31
#lang sicp
(define (product term a next b)
(if (> a b)
1
(* (term a)
(product term (next a) next b))))
(define (product-iter term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (* result (term a)))))
(iter a 1))
(define (factorial n)
(product-iter identity 1 inc n))
(factorial 5)
(define (pi-wallis n)
(define (wallis-term-next t)
(if (= (- (cdr t) (car t)) 1)
(cons (+ (car t) 2) (cdr t))
(cons (car t) (+ (cdr t) 2))))
(define (wallis-term k)
(define (iter i wk)
(if (< i k)
(iter (inc i) (wallis-term-next wk))
(/ (car wk) (cdr wk))))
(iter 1 (cons 2 3)))
(* 4. (product wallis-term 1 inc n)))
(pi-wallis 1000) ;3.1431607055322663
(define (pi-wallis2 n)
(define (wallis-term k)
(/ (* 2 (+ 1 (floor (/ k 2))))
(- (* 2 (+ 1 (ceiling (/ k 2)))) 1))) ;吐槽一下，为啥不叫ceil
(* 4. (product wallis-term 1 inc n)))
(pi-wallis2 1000) ;3.1431607055322663
wiki里一种的算法
(define (pi-term n)
(if (even? n)
(/ (+ n 2) (+ n 1))
(/ (+ n 1) (+ n 2))))
1.32
#lang sicp
(define (sum term a next b)
(if (> a b)
0
(+ (term a)
(sum term (next a) next b))))
(define (product term a next b)
(if (> a b)
1
(* (term a)
(product term (next a) next b))))
(define (accumulate combiner null-value term a next b)
(if (> a b)
null-value
(combiner (term a)
(accumulate combiner null-value term (next a) next b))))
(define (accumulate-iter combiner null-value term a next b)
(define (iter a result)
(if (> a b)
result
(iter (next a) (combiner result (term a)))))
(iter a null-value))
(sum identity 1 inc 10)
(accumulate + 0 identity 1 inc 10)
(accumulate-iter + 0 identity 1 inc 10)
(product identity 1 inc 10)
(accumulate * 1 identity 1 inc 10)
(accumulate-iter * 1 identity 1 inc 10)
1.33
#lang sicp
(define (square x) (* x x))
(define (smallest-divisor n)
(find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b)
(= (remainder b a) 0))
(define (prime? n)
(and (> n 1) (= n (smallest-divisor n))))
(define (filtered-accumulate combiner filter? null-value term a next b)
(define (iter a result)
(if (> a b)
result
(if (filter? a)
(iter (next a) (combiner result (term a)))
(iter (next a) result))))
(iter a null-value))
(define (sum-prime a b)
(filtered-accumulate + prime? 0 square a inc b))
(sum-prime 1 5) ;38
(define (ex1-33-b n)
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))
(define (_filter i)
(= (gcd i n) 1))
(filtered-accumulate * _filter 1 identity 1 inc n))
(ex1-33-b 10) ; 1*3*7*9=189
1.35
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(fixed-point (lambda (x) (+ 1 (/ 1 x)))
1.0)
1.36
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(display guess)
(newline)
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(fixed-point (lambda (x) (/ (log 1000) (log x))) 1.1)
(fixed-point (lambda (x) (+ (* 0.5 x) (/ (log 1000) (* 2 (log x))))) 1.1)
1.1
72.47657378429035
1.6127318474109593
14.45350138636525
2.5862669415385087
7.269672273367045
3.4822383620848467
5.536500810236703
4.036406406288111
4.95053682041456
4.318707390180805
4.721778787145103
4.450341068884912
4.626821434106115
4.509360945293209
4.586349500915509
4.535372639594589
4.568901484845316
4.546751100777536
4.561341971741742
4.551712230641226
4.558059671677587
4.55387226495538
4.556633177654167
4.554812144696459
4.556012967736543
4.555220997683307
4.555743265552239
4.555398830243649
4.555625974816275
4.555476175432173
4.555574964557791
4.555509814636753
4.555552779647764
4.555524444961165
4.555543131130589
4.555530807938518
4.555538934848503
1.1
36.78828689214517
19.352175531882512
10.84183367957568
6.870048352141772
5.227224961967156
4.701960195159289
4.582196773201124
4.560134229703681
4.5563204194309606
4.555669361784037
4.555558462975639
4.55553957996306
4.555536364911781
1.37
(define (cont-frac n d k) ;从上到下
(define (frac i k)
(if (= k 1)
(/ (n i) (d i))
(/ (n i) (+ (d i) (frac (+ i 1) (- k 1))))))
(frac 1 k))
(cont-frac (lambda (i) 1.0) (lambda (i) 1.0) 100)
(define (cont-frac-iter n d k) ;从下到上
(define (iter i res)
(if (< i k)
(iter (+ i 1) (/ (n (- k i)) (+ (d (- k i)) res)))
res))
(iter 1 (/ (n k) (d k))))
(cont-frac-iter (lambda (i) 1.0) (lambda (i) 1.0) 100)
(cont-frac-iter (lambda (i) 1.0) (lambda (i) 1.0) 10)
(cont-frac-iter (lambda (i) 1.0) (lambda (i) 1.0) 11)
;0.6180339887498948
;0.6180339887498948
;0.6179775280898876
;0.6180555555555556
1.38
(define (d i)
(cond ((= i 1) 1)
((= i 2) 2)
((= (remainder (- i 2) 3) 0) (+ 2 (* 2 (/ (- i 2) 3))))
(else 1)))
(define (euler-e)
(+ 2 (cont-frac-iter (lambda (i) 1.0) d 100)))
(euler-e)
;2.7182818284590455
1.39
(define (tan-cf x k)
(define (iter i res)
(if (< i k)
(iter (+ i 1) (/ (square x) (- (- (* 2 (- k i)) 1) res)))
res))
(/ (iter 0.0 (square x)) x))
(tan-cf 1 1000)
(tan 1)
;1.557407724654902
;1.5574077246549023
利用先前定义的cont-frac.
(define (tan-cf-2 x k)
(let ((xx (- (square x))))
(cont-frac (lambda (i) (if (= i 1) x xx))
(lambda (i) (- (* 2 i) 1))
k)))
(tan-cf-2 1. 100) ;1.557407724654902
1.40
(define (cubic a b c)
(lambda (x) (+ (* x x x) (* a x x) (* b x) c)))
(newtom-method (cubic 1 1 1) 1)
1.41
(define (double f)
(lambda (x) (f (f x))))
((double inc) 1) ;3
(((double (double double)) inc) 5) ;21
1.42
(define (compose f g)
(lambda (x) (f (g x))))
((compose square inc) 6) ;49
1.43
(define (repeated f n)
(if (= n 1)
f
(compose f (repeated f (- n 1)))))
((repeated square 2) 5) ;625
1.44
(define (smooth f)
(lambda (x)
(/ (+ (f (- x dx)) (f x) (f (+ x dx))) 3)))
(define (smooth-n f n)
((repeated smooth n) f))
1.45
使用平均阻尼是为了加速迭代收敛的速度，画图研究可知把函数$f(x)=\frac{A}{x^{n-1}}$变换到最小值点在不动点(与直线$y=x$的交点)的左边时收敛要快一点。
比如要求$2$的$4$次方根，要找不动点的函数就是$f(x)=\frac{2}{x^3}$.
如果不用平均阻尼的话，迭代过程长这样：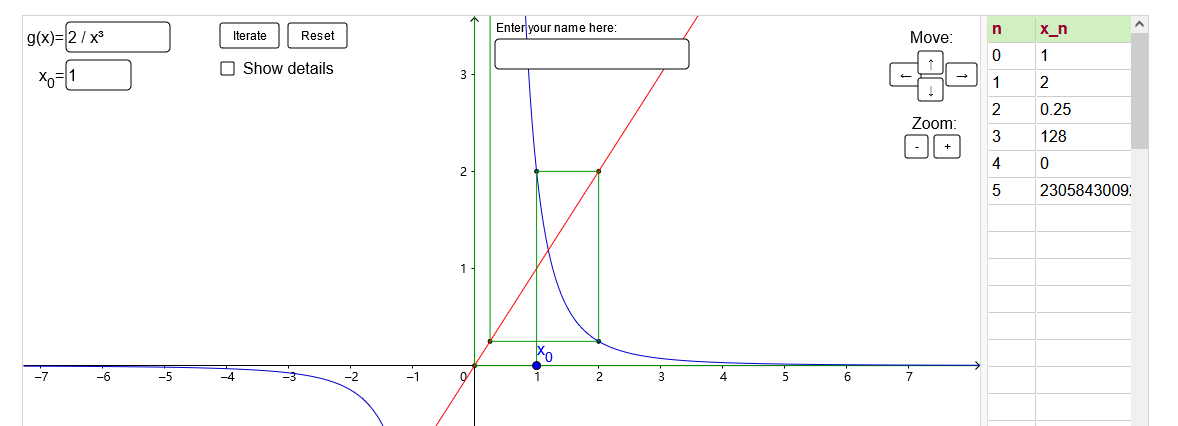
，可见很难收敛.
使用一次平均阻尼后函数为$f_1(x)=\frac{1}{2}x+\frac{1}{x^3}$，迭代过程长这样：
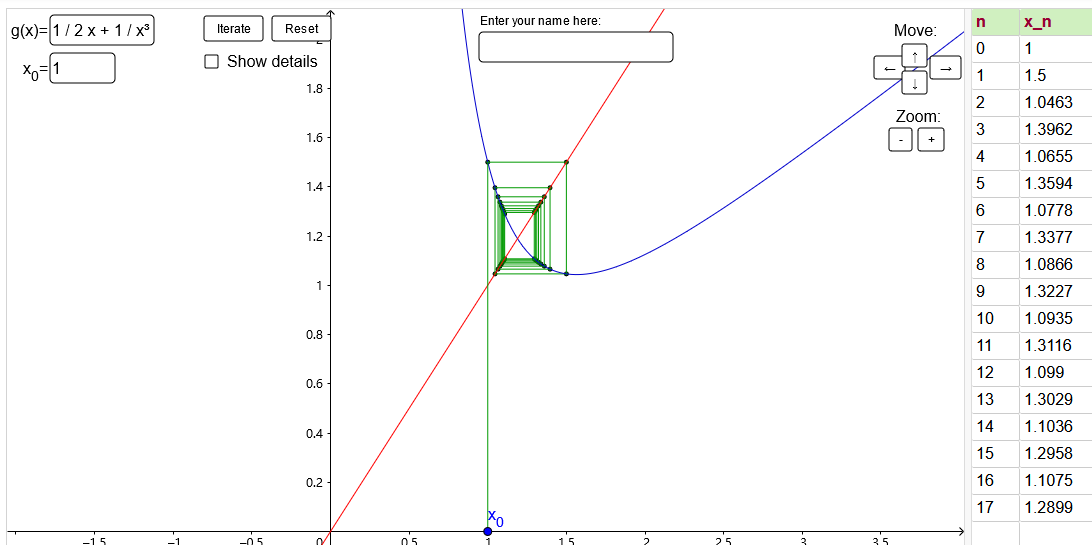
首先可以看到函数有最小值点了，不过迭代过程是一个非常慢的转圈圈的过程.
使用两次平均阻尼后函数为$f_2(x)=\frac{3}{4}x+\frac{1}{2x^3}$
迭代过程长这样：
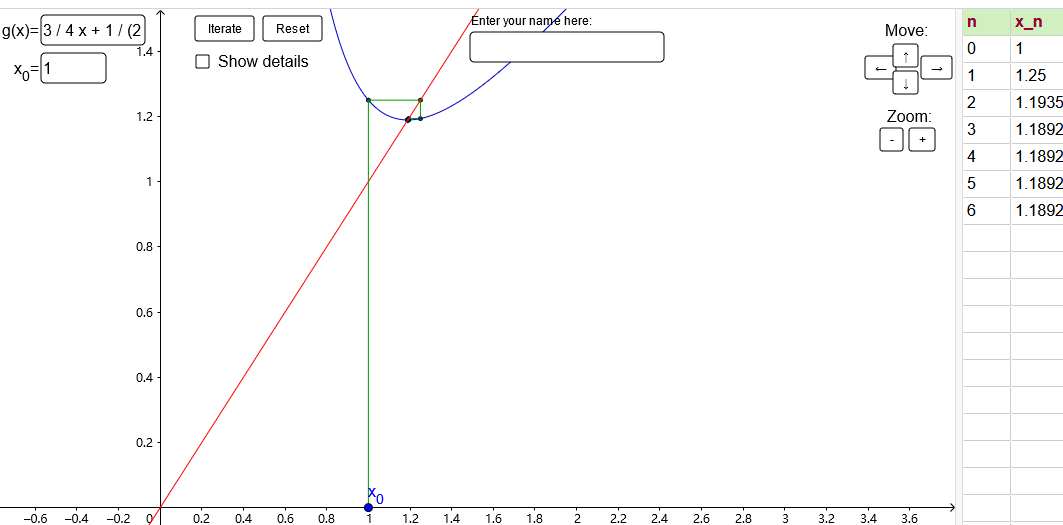
可以看到几下就收敛了.
所以盲猜把函数$f(x)=\frac{A}{x^{n-1}}$变换到最小值点在不动点的左边时收敛会快一点.
对$f(x)=\frac{A}{x^{n-1}}$施加m次average-damp操作后得到
\[F(x)=(1-\frac{1}{2^m})x+\frac{A}{2^m}\frac{1}{x^{n-1}}\]求解$\frac{dF(x)}{dx}=0$可得最小值点横坐标为
\[\sqrt[n]{\frac{A(n-1)}{2^m-1}}\]而不动点横坐标为$\sqrt[n]{A}$
要求最小值点在不动点的左边，所以有不等式
\[\sqrt[n]{\frac{A(n-1)}{2^m-1}}\leq\sqrt[n]{A}\]得\(m\geq\log_2n\)
参考链接：
Google到的画上面蛛网图的工具 https://www.geogebra.org/m/uvsfvNDt
知乎 SICP 1.45证明？
日本的一篇博客 SICP問題1.45の回答と説明（SICP1.3.4, ex1.45）
特别鸣谢：谢惠民等.《数学分析习题课讲义（上册）》第49-51页让我进一步了解了不动点，以及“蛛网（cobweb）工作法”的概念。
#lang sicp
(define (square x) (* x x))
(define (average x y) (/ (+ x y) 2))
(define tolerance 0.00001)
(define (fixed-point f first-guess)
(define (close-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
(define (try guess)
(let ((next (f guess)))
(if (close-enough? guess next)
next
(try next))))
(try first-guess))
(define (average-damp f)
(lambda (x) (average x (f x))))
(define (fixed-point-of-transform g transform guess)
(fixed-point (transform g) guess))
(define (compose f g)
(lambda (x) (f (g x))))
(define (repeated f n)
(if (= n 1)
f
(compose f (repeated f (- n 1)))))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
(else (* b (fast-expt b (- n 1))))))
(define (nth-root x n)
(fixed-point-of-transform (lambda (y) (/ x (fast-expt y (- n 1))))
(repeated average-damp (ceiling (/ (log n) (log 2))))
1.0))
(nth-root 2 4) ;1.189207115002721
(nth-root 5 32)
1.46
#lang sicp
(define (average x y) (/ (+ x y) 2))
(define tolerance 0.00001)
(define (iterative-improve good-enough? improve)
(define (try guess)
(let ((next (improve guess)))
(if (good-enough? guess next)
next
(try next))))
try)
(define (fixed-point f first-guess)
(define (good-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
((iterative-improve good-enough? f) first-guess))
(define (my-sqrt x)
(define (improve y)
(average y (/ x y)))
(define (good-enough? v1 v2)
(< (abs (- v1 v2)) tolerance))
((iterative-improve good-enough? improve) x))
(fixed-point cos 1.0)
(my-sqrt 2.0)