$\gdef\lrb#1{\lbrace#1\rbrace}$ $\gdef\leq{\leqslant}$ $\gdef\geq{\geqslant}$ $\gdef\qed{~\tag*{\Large□}}$ $\gdef\s{\cdots}$ $\gdef\ip{2\pi i}$ $\gdef\C{\mathbb{C}}$ $\gdef\fqn{F^n_q}$ $\gdef\ol#1{\overline{#1}}$
设$S$和$T$是有限集合,$S$到$T$的函数表示为$f:S\rarr T$. 令$s=|S|,t=|T|$,因为对$S$中每个元素均有$t$种可能取值,所以从$S$到$T$的函数个数共有$t^s$个.
定义 一个$n$元布尔函数指从$F^n_2$到$F_2$的函数$f=f(x_1,...,x_n):F^n_2\rarr F_2$. 这样的函数共有$2^{2^n}$个,以$B_n$表示所有$n$元布尔函数组成的集合.
布尔函数的推广:
$1.\quad F_2\rarr F_q$,$q$是素数,函数$f=f(x_1,...,x_n):F_q^n\rarr F_q$即有限域$F_q$上的$n$元广义布尔函数. 这样的函数有$q^{q^n}$个. 以$B_{n,q}$表示所有这样函数的集合,则$B_n=B_{n,2}$.
$2.\quad$环$Z_m(m\geqslant2)$上的$n$元广义布尔函数,$f=f(x_1,...,x_n):Z^n_m\rarr Z_m$. 这样的函数有$m^{m^n}$个,以$B_{n,(m)}$表示这样函数的集合,当$m$为素数$p$时,$Z_p=F_p$,则$B_{n,(p)}=B_{n,p}$.
$n$元广义布尔函数的运算
设$S$为$F_q$或$Z_m,~f(x_1,\s,x_n)$和$g(x_1,\s,x_n)$是$S$上的广义布尔函数. $f,g:S^n\rarr S$.
定义 $f\pm g$和$fg$为$S$上的广义布尔函数,对$(a_1,\s,a_n)\in S^n$
$$
\begin{aligned}
(f\pm g)(a_1,\s,a_n)&=f(a_1,\s,a_n)\pm g(a_1,\s, a_n)\\
fg(a_1,\s,a_n)&=f(a_1,\s,a_n)g(a_1,\s,a_n)
\end{aligned}
$$ $B_{n,q}$和$B_{n,(m)}$均是交换环,零元素为$f(x_1,\s,x_n)\equiv0$,恒等元为$f(x_1,\s,x_n)\equiv1$.
多项式环$F_q[x_1,\s,x_n]$中每个多项式都可以看成是$F_q$上的$n$元广义布尔函数,则有环同态$$ \varphi:F_q[x_1,\s,x_n]\rarr B_{n,q} $$ $\varphi$不是单同态. 比如$f(x_1,\s,x_n)=x_1^q,g(x_1,\s,x_n)=x_1$. 对$a\in F_q$均有$a^q=a$,所以对每个向量$(a_1,\s,a_n)\in F^q_n$有$f(a_1,\s,a_n)=a^q_1=a_1=g(a_1,\s,a_n)$. 即$f$和$g$是$B_{n,q}$中同一个广义布尔函数.
引理 环同态$\varphi$是满同态并且核$Ker(\varphi)$是由$x^q_1-x_1,\s,x^q_n-x_n$生成的$F_q[x_1,\s,x_n]$中的理想,于是有环的同构$$
\frac{F_q[x_1,\s,x_n]}{(x_1^q-x_1,\s,x_n^q-x_n)}\cong B_{n,q}
$$
证明:思路:(1)证$\varphi$是满的,即每个广义布尔函数$f=f(x_1,\s,x_n)\in B_{n,q}$都可表示成多项式.
考虑$F(x_1,\s,x_n)=\displaystyle\sum_{(c_1,\s,c_n)\in F_q^n}f(c_1,\s,c_n)(1-(x_1-c_1)^{q-1})\s(1-(x_n-c_n)^{q-1}),~F\in F_q[x_1,\s,x_n]$
对于$(a_1,\s,a_n)\in F^n_q$ $$
(1-(a_1-c_1)^{q-1})(1-(a_2-c_2)^{q-1})\cdots(1-(a_n-c_n)^{q-1})=\begin{cases}
0~~(c_1,\s,c_n)\neq(a_1,\s,a_n)\\
1~~(c_1,\s,c_n)=(a_1,\s,a_n)
\end{cases}
$$ 即$F(a_1,\s,a_n)=f(a_1,\s,a_n)\quad(_1,\s,a_n)\in F^n_q)$即$f$可表示成函数$F$.
(2) $x_1^q-x_1,\s,x_n^q-x_n$是$B_{n,q}$中恒为0的函数,因此属于$Ker(\varphi)$. 由它们生成的理想$I=(x_1^q-x_1,\s,x_n^q-x_n)$包含在$Ker(\varphi)$中,由环的同态基本定理,有环的满同态$$
\widetilde{\varphi}:\frac{F_q[x_1,\s,x_n]}{I}\rarr B_{n,q}
$$ 在商环$R=\frac{F_q[x_1,\s,x_n]}{I}$中,每个多项式模$I$后,$x^q_i$变为$x_i$,即$m>q-1$时$x^m_i\equiv x_i^{m-(q-1)}~(mod~I)$. 于是$R$中每个多项式表示为$$
g(x_1,\s,x_n)=\sum_{\substack{(l_1,\s,l_n)\in\Z^n\\0\leq l_i\leq q-1}}C_{l_1\s l_n}x_1^{l_1}\s x_n^{l_n}\quad(C_{l_1\s l_n}\in F_q)\tag{a}
$$ 单项式$x_1^{l_1}\s x_n^{l_n}$共有$q^n$个,对每个$(l_1,\s,l_n)$,$C_{l_1\s l_n}$有$q$种取法,即$|R|\leq q^{q^n}$. 而$\widetilde{\varphi}:R\rarr B_{n,q}$是满射,$|B_{n,q}|=q^{q^n}$,则$|R|=q^{q^n}$. $\widetilde{\varphi}$是单射,则$\widetilde{\varphi}$是环同构. $$\qed$$
由于$|R|=q^{q^n}$,则形如$(a)$式的不同多项式是不同的广义布尔函数,上述引理即为:
定理 (1)每个$F_q$上的$n$元布尔函数$f:F_q^n\rarr F_q$均唯一地表示成$(a)$的形式. 即$f$可唯一地表示成多项式$f(x_1,\s,x_n)\in F_q[x_1,\s,x_n]$. 其中$f$对每个$x_i$的次数均$\leq q-1$. 此多项式即为$$ F(x_1,\s,x_n)=\sum_{(c_1,\s,c_n)\in F_q^n}f(c_1,\s,c_n)(1-(x_1-c_1)^{q-1})\s(1-(x_n-c_n)^{q-1}) $$ (2)$B_{n,q}$是以$x_1^{l_1}x_2^{l_2}\s x_n^{l_n}~(0\leq l_1,\s,l_n\leq q-1)$为基的$F_q$上$q^n$维向量空间.
推论 $q=2$时$1-(x-c)^{q-1}=1+x+c$,每个$n$元布尔函数$f:F^n_2\rarr F_2$可唯一地表示成多项式$$ \begin{aligned} f(x_1,x_2,\s,x_n)&=\sum_{0\leq l_1,l_2,\s,l_n\leq 1}C_{l_1l_2\s l_n}x_1^{l_1}x_2^{l_2}\s x_n^{l_n}~~(C_{l_1l_2\s l_n}\in F_2)\\ &=a_0+a_1x_1+\s+a_nx_n+a_{12}x_1x_2+\s+a_{n-1,n}x_{n-1}x_n+\\ &+a_{123}x_1x_2x_3+\s+a_{12\s n}x_1x_2\s x_n~~\in F_2[x_1,x_2,\s,x_n] \end{aligned} $$ 事实上,$$ f(x_1,x_2,\s,x_n)=\sum_{(c_1,c_2,\s,c_n)\in F^n_2}f(c_1,c_2,\s,c_n)(x_1+c_1+1)(x_2+c_2+1)\s(x_n+c_n+1), $$ 且$n$元布尔函数环$B_n$是以$$ \lrb{1,x_1,\s,x_n,x_1x_2,\s,x_{n-1}x_n,x_1x_2x_3,\s,x_1x_2\s x_n} $$为基的$F_2$上$2^n$维向量空间.
例1 对于二元布尔函数$f(0,0)=f(1,1)=1,f(0,1)=f(1,0)=0$,它的多项式为$$ \begin{aligned} f(x_1,x_2)&=\sum_{(c_1,c_2)\in F^2_2}f(c_1,c_2)(x_1+c_1+1)(x_2+c_2+1)\\ &=(x_1+1)(x_2+1)+x_1x_2\\ &=x_1x_2+x_1+x_2+1+x_1x_2\\ &=1+x_1+x_2 \end{aligned} $$
例2 对于二元布尔函数$f(0,0)=0,f(1,0)=f(0,1)=f(1,1)=1$ $$ \begin{aligned} f(x_1,x_2)&=\sum_{c_1,c_2\in F^2_2}f(c_1,c_2)(x_1+c_1+1)(x_2+c_2+1)\\ &=(x_1+1+1)(x_2+1)+(x_1+1)(x_2+1+1)+(x_1+1+1)(x_2+1+1)\\ &=x_1(x_2+1)+(x_1+1)x_2+x_1x_2\\ &=x_1+x_2+x_1x_2 \end{aligned} $$
对于$F_3$上二元广义布尔函数
$f(x_1,x_2)=\displaystyle\sum_{c_1,c_2\in F^2_3}f(c_1,c_2)(1-(x_1-c_1)^2)(1-(x_2-c_2)^2)$
例3 $f(0,0)=f(1,1)=1,f(2,2)=2,f(i,j)=0~(i,j\in F_3,i\neq j)$,它的多项式为$$ \begin{aligned} f(x_1,x_2)&=(1-x^2_1)(1-x^2_2)+(1-(x_1-1)^2)(1-(x_2-1)^2)\\ &+2(1-(x_1-2)^2)(1-(x_2-2)^2)\\ &=1-x_1^2-x_2^2+x^2_1x^2_2+x_1x_2+x_1x_2^2+x_1^2x_2+x_1^2x_2^2\\ &-x_1x_2+x_1x_2^2+x_1^2x_2-x_1^2x_2-x_1^2x_2^2\\ &=1-x_1^2+x_2^2-x_1x_2^2-x_1^2x_2+x_1^2x_2^2 \end{aligned} $$
例4 对$F_3$上的二元布尔函数$f(0,0)=f(1,1)=f(2,2)=0,f(1,2)=1,f(2,1)=2,f(0,1)=1,f(1,0)=2,f(0,2)=1,f(2,0)=2$ $$ \begin{aligned} f(x_1,x_2)&=\sum_{(c_1,c_2)\in F^2_3}f(c_1,c_2)(1-(x_1-c_1)^2)(1-(x_2-c_2)^2)\\ &=(1-x_1^2)(1-(x_2-1)^2)+2(1-(x_1-1)^2)(1-x_2^2)\\ &+(1-x_1^2)(1-(x_2-2)^2)+2(1-(x_1-2)^2)(1-x_2^2)\\ &+(1-(x_1-1)^2)(1-(x_2-2)^2)+2(1-(x_1-2)^2)(1-(x_2-1)^2)\\ &=-x_1^2+x_2^2-x_1x_2^2+x_1^2x_2 \end{aligned} $$ 注:对$m\geq2$,当$m$不是素数时,$Z_m$上每个$n$元广义布尔函数不一定可表示成多项式,例:$m=8$,对每个$a\in Z_8$有$a^5=a^3$的多项式函数$f:Z_8\rarr Z_8$的个数不超过$8^5$个($Z_8[x]$中次数小于等于4的多项式个数),但是$Z_8$上的一元广义布尔函数共有$8^8$个,其中必有不能表示成多项式的。
对每个函数$f:S\rarr T$. 若$|S|=s$,按其次序排列$S=\lrb{\alpha_1,\s,\alpha_s}$. $f$表示成$T$中长为$s$的序列$f=(f(\alpha_1),\s,f(\alpha_s))~~,f(\alpha_i)\in T$.
当$S=\Z^n_m$时,将$0,1,\s,m^n-1$用$m$进制表示成$$
i=i_0+i_1m+\s+i_{n-1}m^{n-1},0\leq i_0,i_1,\s,i_{n-1}\leq m-1\quad(0\leq i\leq m^n-1)
$$ 则$(i_0,i_1,\s,i_{n-1})$是$\Z^n_m$中全部元素,所以$\Z_m$上一个$n$元布尔函数$f:\Z^n_m\rarr \Z_m$可表示成$$
(f(0_0,\s,0_{n-1}),f(1_0,\s,1_{n-1}),\s,f((m^n-1)_0,\s,(m^n-1)_{n-1}))
$$ 其中$$
\begin{aligned}
(0_0,0_1,\s,0_{n-1})&=(0,0,\s,0)\\
(1_0,1_1,\s,1_{n-1})&=(1,0,\s,0),\s,\\
((m^n-1)_0,(m^n-1)_1,\s,(m^n-1)_{n-1}))&=(m-1,m-1,\s,m-1)
\end{aligned}
$$
例 $Z^2_2$,将$0,1,2,3$用2进制表示$$ \begin{aligned} 0=0+0\cdot2\quad(0_0,0_1)=(0,0)\\ 1=1+0\cdot2\quad(1_0,1_1)=(1,0)\\ 2=0+1\cdot2\quad(2_0,2_1)=(0,1)\\ 3=1+1\cdot2\quad(3_0,3_1)=(1,1) \end{aligned} $$
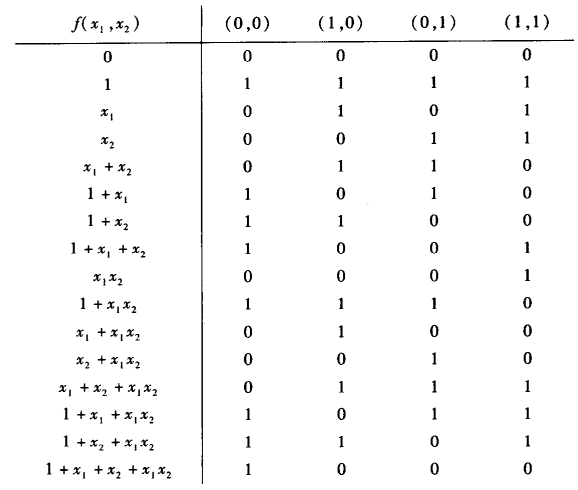
例 2元布尔函数$f=f(x_1,x_2):F^2_2\rarr F_2$共有$2^{2^2}=16$个,如下表:

通信的应用中,$n$元布尔函数的其他表示方式
例:开关线路中,基本电子元件有
(1) 非门 $f:F_2\rarr F_2,f(0)=1,f(1)=0,f(x)=x+1$,表示成$f(x)=\overline{x}$
(2) 与门 $f:F_2^n\rarr F_2.~f(a_1,\s,a_n)=\begin{cases}1&,~a_1=\s=a_n=1\\0&,~otherwise\end{cases}$. 即$f(x_1,\s,x_n)=x_1\s x_n$,表示成$f(x_1,\s,x_n)=x_1\wedge x_2\wedge\s\wedge x_n$
(3) 或门 $f:F_2^n\rarr F_2,~f(a_1,\s,a_n)=\begin{cases}0&,~a_1=\s=a_n=0\\1&,~otherwise\end{cases}$即$f(x_1,\s,x_n)=(x_1+1)\s(x_n+1)+1$,表示为$x_1\vee x_2\vee\s\vee x_n$.
性质:$$ \begin{aligned} \overline{x_1\wedge x_2}=\overline{x_1}\vee\overline{x_2},~\overline{x_1\vee x_2}=\overline{x_1}\wedge\overline{x_2}\\ x\wedge\bar{x}=0,x\vee\bar{x}=1,0\vee x=x,1\wedge x=x\\ x_1\wedge(x_2\vee x_3)=(x_1\wedge x_2)\vee(x_2\wedge x_3)\\ x_1\vee(x_2\wedge x_3)=(x_1\vee x_2)\wedge(x_1\vee x_3) \end{aligned} $$
每个$n$元布尔函数$f:F_2^n\rarr F_2$都可用门元件表示$$ f(x_1,\s,x_n)=\underset{(c_1,\s,c_n)\in F^n_2}{\vee}f(c_1,\s,c_n)(x_1+c_1+1)\wedge(x_2+c_2+1)\wedge\s\wedge(x_n+c_n+1) $$ 其中$x+c+1=\begin{cases}x\quad c=1\\ \bar{x}\quad c=0\end{cases}$
例 $f(x_1,x_2)=x_1+x_2:F^2_2\rarr F_2$,则$f(0,0)=f(1,1)=0,f(1,0)=f(0,1)=1$,则$x_1+x_2=(\overline{x_1}\wedge x_2)\vee(x_1\wedge\overline{x_2})$
对于正整数$m\geq2$,令$\zeta_m=e^\frac{\ip}{m}~(i=\sqrt{-1})$
定义 (1)对每个正整数$m\geq2,\Z_m$上的$n$广义布尔函数$f=f(x_1,x_2,\s,x_n):\Z^n_m\rarr\Z_m$的Walsh变换指函数$W_f:\Z^n_m\rarr\C$,其中对$y=(y_1,\s,y_n)\in\Z^n_m$ $$
W_f(y)=\sum_{x=(x_1,\s,x_n)\in\Z^n_m}\zeta_m^{f(x)-x\cdot y}
$$ 其中$x\cdot y=x_1y_1+\s+x_ny_n\in\Z_m$.
注:若$a\equiv b(mod~m)$则$\zeta^a_m=\zeta^b_m$,对于$\Z_m$中元素$a$可定义$\zeta_m^a$
(2) 对于有限域$F_q,~q=p^l$($p$为素数,$l\geq1$),设$T$表示$F_q$对$F_p$的迹函数,则$n$元广义布尔函数$f=f(x_1,\s,x_n):F^n_q\rarr F_q$的Walsh变换是函数$W_f:F^n_q\rarr\C$,其中对每个向量$y=(y_1,\s,y_n)\in F^n_q$ $$
W_f(y)=\sum_{x=(x_1,\s,x_n)\in F^n_q}\overline{\chi}_y(x)\zeta^{T(f(x))}_p=\sum_{x\in F^q_n}\zeta^{T(f(x)-x\cdot y)}_p
$$ 其中$\chi_y$是$F_q$的加法特征,对$x\in F_q^n,~\chi_y(x)=\zeta^{T(x\cdot y)}_p,~(x\cdot y=x_1y_1+\s+x_ny_n\in F_q)$. 当$m=p$(素数)时$\Z_p=F_p$,上述两个定义一致.
Walse反变换
引理:(1)对于$F_q$上$n$元广义布尔函数$f:F^n_q\rarr F_q,~f=f(x)=f(x_1,\s,x_n)$. $$
\zeta_p^{T(f(x))}=q^{-n}\sum_{g\in F^n_q}\chi_y(x)W_f(y)=q^{-n}\sum_{y\in F^n_q}W_f(y)\zeta^{T(x\cdot y)}_p
$$ 证明:$$
\begin{aligned}
&\sum_{y\in F^n_q}W_f(y)\chi_y(x)\\
&=\sum_{y\in F^n_q}\chi_y(x)\sum_{z\in F^n_q}\overline{\chi_y}(x)\zeta^{T(f(z))}_p\\
&=\sum_{z\in F^n_q}\zeta^{T(f(z))}_p\sum_{y\in F^n_q}\chi_y(x)\overline{\chi_y}(z)
\end{aligned}
$$ 而$\sum_{y\in F^n_q}\chi_y(x)\overline{\chi_y}(z)=\begin{cases}0\quad&x\neq z\\q^n\quad&x=z\end{cases}$(特征的正交性),即上式$=q^n\zeta^{T(f(x))}_p$.
(2) 对于$\Z_m$上的$n$元广义布尔函数$f:\Z^n_m\rarr\Z_m,~f=f(x)=f(x_1,\s,x_n)$. $$
\zeta^{f(x)}_m=m^{-n}\sum_{y\in\Z^n_m}W_f(y)\zeta^{x\cdot y}_m
$$ 特殊情况:$m=q=2,~n$元布尔函数$f=f(x)=f(x_1,\s,x_n):F_2^n\rarr F_2$的Walsh变换$W_f:F^n_q\rarr\Z$和它的反变换为$$
\begin{aligned}
W_f(y)=\sum_{x\in F^n_2}(-1)^{f(x)+x\cdot y}\\
(-1)^{f(x)}=2^{-n}\sum_{y\in F^n_2}W_f(y)(-1)^{x\cdot y}
\end{aligned}
$$
性质
布尔函数Walsh变换的性质:
设$f$和$g$是$n$元布尔函数,即$f,g\in B_n$则
(1) $\displaystyle\sum_{y\in F^n_2}W_f(y)\overline{W_f(y+c)}=\begin{cases}2^{2n}\quad&c=(0,\s,0)\in F^n_2\\0&otherwise\end{cases}$
(2)$W_{f+g}(y)=2^{-n}\displaystyle\sum_{a\in F_2^n}W_f(a)W_g(y-a)$
(3)对$a\in F_2^n,~g(x)=f(x+a)$,则$W_g(y)=(-1)^{a\cdot y}W_f(y)$
定义 对于每个$n$元布尔函数$f=f(x)=f(x_1,\s,x_n):F^n_2\rarr F_2$,以$W_H(f)$表示函数$f$取值为1的个数,称为$f$的汉明权,$W_H(f)=\#\lrb{a=(a_1,\s,a_n)\in F_2^n:f(a)=1}$,$f$取值为0的个数是$2^n-W_H(f)$.
当$W_H(f)=2^{n-1}$,此时$f$取值为0和1的个数相等,称布尔函数$f$是平衡的.
定义 $f$和$g$的汉明距离$$
d_H(f,g)=W_H(f-g)\#\lrb{a=(a_1,\s,a_n)\in F_2^n:f(a)\neq g(a)}
$$ 可用来衡量$f$和$g$相差的程度.
引理 设$f,g\in B_n,~W_f:F^n_2\rarr\Z$是$f$的Walsh变换,则(1) $W_f(0)=2^n-2W_H(f)$,$f$是平衡的当且仅当$W_f(0)=0$. (2)$W_{f+g}(0)=2^n-2d_H(f,g)$
证明:(1) $W_f(0)=\displaystyle\sum_{x\in F^n_2}(-1)^{0\cdot x+f(x)}=\sum_{x\in F^n_2}(-1)^{f(x)}$
$=\displaystyle\sum_{\substack{x\in F^n_2\\f(x)=0}}1-\sum_{\substack{x\in F_2^n\\f(x)=1}}1=(2^n-W_H(f))-W_H(f)=2^n-2W_H(f)$
(2)$W_{f+g}(0)=2^n-2W_H(f+g)=2^n-2d_H(f,g)$(二元域里f+g=f-g)
因此$f+g$的Walsh变换$W_{f+g}$在$0=(0,\s,0)\in F^n_2$处的值$W_{f+g}(0)~(\in\Z)$可以表示$f$和$g$的汉明距离
$d_H(f,g)=\frac{2^n-W_{f+g}(0)}{2}$ ($W_{f+g}(0)$是偶数,$-2^n\leq W_{f+g}(0)\leq 2^n$)
$d_H(f,g)=0$当且仅当$W_{f+g}(0)=2^n\quad(f=g)$
$d_H(f,g)=2^n$当且仅当$W_{f+g}(0)=-2^n\quad$($f=g+1$汉明距离最大)
对每个向量$a=(a_1,\s,a_n)\in F_2^n$和$c\in F_2^n$
布尔函数$f(x_1,\s,x_n)=a_1x_1+\s+a_nx_n+c=a\cdot x+c$叫做仿射函数(次数$\leq1$的布尔函数)
$c=0$时$f$叫做线性函数.
定义 对于$1\leq t\leq n$,$n$元布尔函数$f(x)=f(x_1,\s,x_n)$叫做$t$阶相关免疫的,是指对每个$a=(a_1,\s,a_n)\in F^n_2,~1\leq W_H(a)\leq t$,均有$d_H(f,a\cdot x)=2^{n-1}$,即$$ W_f(a)=\sum_{x\in F^n_2}(-1)^{f(x)+a\cdot x}=0 $$ (对每个$a\in F^n_2,1\leq W_H(a)\leq t$)
设$q\geq2,f=f(x_1,\s,x_n):\Z^m_q\rarr\Z_q$是$\Z_q$上的$m$元广义布尔函数,对于它的Walsh变换$$
W_f(y)=\sum_{x\in\Z^m_q}\zeta_q^{f(x)-x\cdot y}\in\C\quad(y=(y_1,\s,y_n)\in\Z^m_q)
$$ 则$\displaystyle\sum_{y\in\Z^m_q}|W_f(y)|^2=q^{2m}$,则$q^m$个Walsh函数值$|W_f(y)|^2$平均值为$\frac{q^{2m}}{q^m}=q^m$.
当这些均值均相等时,即所有$|W_f(y)|$均为$q^\frac{m}{2}$时,$f(x)$与所有仿射函数$g(x)=x\cdot y+b~(y\in\Z^m_q,b\in\Z_q)$的距离都相等,这种函数很有应用价值.
定义 $\Z_q$上的$m$元广义布尔函数$f:\Z^m_q\rarr\Z_q$叫做广义bent函数,是指对每个$y\in\Z^m_q$ $$ |W_f(y)|=|\sum_{x\in\Z^m_q}\zeta_q^{f(x)-x\cdot y}|=q^\frac{m}{2} $$ 当$q=2$时,$f$叫做bent函数.
基本问题:(1)对于哪些$q\geq2$和$m\geq1$,存在$\Z_q$上的$m$元广义bent函数.
$\qquad\qquad,$(2)若存在的话,试构作全部广义bent函数并分类.
对于bent函数,$m$元bent函数$f:\Z_2^m\rarr\Z_2$ $$ |W_f(y)|=|\sum_{x\in\Z_2^m}(-1)^{f(x)-x\cdot y}|=2^\frac{m}{2}\quad(y\in\Z_2^m) $$ 而$W_f(y)\in\Z$,可知$m$必为偶数,即$m$为奇数时不存在$m$元bent函数.
定理 (1)若$f:\Z_2^m\rarr\Z_2$和$g:\Z_2^n\rarr\Z_2$分别是$m$元和$n$元bent函数,则$h:\Z_2^{m+n}\rarr\Z_2$. $$
h(x_1,\s,x_{m+n})=f(x_1,\s,x_m)+g(x_{m+1},\s,x_{m+n})
$$ 是$m+n$元bent函数.
证明:$|W_f(y_1)|=2^\frac{m}2~(y_1\in\Z_2^m)$,$|W_g(y_2)|=2^\frac{n}{2}~(y_2\in\Z_2^n)$
于是对于$y=(y_1,y_2)\in\Z_2^{m+n},~y_1\in\Z_2^m,y_2\in\Z_2^n$ $$
\begin{aligned}
W_h(y)&=\sum_{\substack{x_1\in\Z_2^m\\x_2\in\Z_2^n}}(-1)^{f(x_1)+g(x_2)-x_1\cdot y_1-x_2\cdot y_2}\\
&=\sum_{x_1\in\Z_2^m}(-1)^{f(x_1)-x_1\cdot y_1}\sum_{x_2\in\Z_2^n}(-1)^{g(x_2)-x_2\cdot y_2}\\
&=W_f(y_1)W_g(y_2)
\end{aligned}
$$ 从而$|W_h(y)|=|W_f(y_1)||W_g(y_2)|=2^\frac{m+n}{2}$,即$h$是$m+n$元bent函数.
(2)对每个偶数$m\geq2$,均存在$m$元bent函数.
证明:取$f(x_1,x_2)=x_1x_2$,所有函数$$
x_1x_2+x_1y_1+x_2y_2\quad(y_1,y_2\in\Z_2)
$$ 的取值表为
| $(x_1,x_2)=$ | $(0,0)$ | $(0,1)$ | $(1,0)$ | $(1,1)$ |
| $x_1x_2$ | 0 | 0 | 0 | 1 |
| $x_1x_2+x_1$ | 0 | 0 | 1 | 0 |
| $x_1x_2+x_2$ | 0 | 1 | 0 | 0 |
| $x_1x_2+x_1+x_2$ | 0 | 1 | 1 | 1 |
则对每个$y\in\Z_2^2,~W_f(y)=\pm2,~f=x_1x_2$是二元bent函数,于是对每个偶数$m\geq2$,均存在$m$元bent函数. $$\qed$$
例如:$W_f(y)=\displaystyle\sum_{x\in\Z^2_2}(-1)^{f(x_1,x_2)-(x_1,x_2)\cdot(y_1,y_2)}$,表中值即为指数中的值
第一行,此时$(y_1,y_2)=(0,0)$,$(x_1,x_2)$分别取$(0,0),(0,1),(1,0),(1,1)$得$f(x_1,x_2)-(x_1,x_2)\cdot(y_1,y_2)$的四个值为:$0,0,0,1$,故$W_f(y)=1+1+1-1=2$
第四行,此时$(y_1,y_2)=(1,1)$,$(x_1,x_2)$分别取$4$个值时,$f(x_1,x_2)-(x_1,x_2)\cdot(y_1,y_2)$的四个值为$0,-1,-1,-1$,则$W_f(y)=1-1-1-1=-2$.
对于广义bent函数,即$q\geq3$时
定理 如果$m$为正偶数,或者$q\not\equiv2~(mod~4)$,则存在$\Z_q$上的$m$元广义布尔函数.
注:当$m$为奇数且$q\equiv2~(mod~4)$时,已证明在许多情形下,这种$m$元广义布尔函数不存在(利用代数数论).
证明:分几种情形,第一种:$m$为正偶数.
引理1 设$m=2k~(k\geq1),~q\geq2$,对任何$\varphi:Z_q^k\rarr\Z_q$,令$f=f(x_1,x_2):\Z^m_q\rarr\Z_q,~f(x_1,x_2)=x_1\cdot x_2+\varphi(x_1)~((x_1,x_2)\in\Z_q^k)$,则$f$为$\Z_q$上$m$元广义bent函数.
证明:对于$y=(y_1,y_2),~y_1,y_2\in\Z_q^k$. $$
\begin{aligned}
W_f(y)&=\sum_{x_1,x_k\in\Z_q^k}\zeta_q^{x_1\cdot x_2+\varphi(x_1)-x_1\cdot y_1-x_2\cdot y_2}\\
&=\sum_{x_1\in\Z_q^k}\zeta_q^{\varphi(x_1)-x_1y_1}\sum_{x_2\in\Z_q^k}\zeta_q^{x_2\cdot(x_1-y_2)}\\
&=q^k\sum_{\substack{x_1\in\Z_q^k\\x_1=y_2}}\zeta_q^{\varphi(x_1)-x_1\cdot y_1}=q^k\zeta_q^{\varphi(y_2)-y_2\cdot y_1}
\end{aligned}
$$ 则$|W_f(y)|=q^k=q^\frac{m}{2}$,即$f$为广义bent函数.
第二种:$q\not\equiv2~(mod~4)$的情形,即$\forall m\in\Z^\ast,~Z_q$上$m$元广义bent函数均存在.
只需证明$\Z_q$上一元广义bent函数$f:\Z_q\rarr\Z_q$存在,进而$\Z_q$上$n_1$元和$n_2$元广义bent函数均存在,类似前面的定理可以证明$\Z_q$上$n_1+n_2$元广义bent函数也存在.
对于$q\not\equiv2~(mod~4)$分4种情况:
(1) q为奇数 (2)$q=2^{2k}~(k\geq1)$
(3) $q=2^{2k+1}~(k\geq1)$ (4) $q=2^l\cdot r~(2\not|r\geq3,l\geq2)$
$q$为$4$的整数倍,均可表示为$2^l\cdot y~(l\geq2)$,而$2^l\cdot y$均可表示为$2^l$的奇数倍,因此若$y$为偶数,令$y=2s$,则$2^l\cdot 2s=2^{l+1}\cdot s$,若$s$为偶数,继续这个过程直到$s_i$为奇数,得$2^l\cdot y=2^l\cdot r$,其中$2\not|r\geq1,~l\geq2$.
而对$r=1$的情况,即$2^l\cdot y=2^l=\begin{cases}2^{2k}\\2^{2k+1}\end{cases},~k\geq1$,由此将$q\not\equiv2~(mod~4)$分成4类.
(1)$q$为奇数
引理2 设$q$为奇数,$q\geq3,~f:\Z_q\rarr\Z_q$为$f(x)=x^2$则$f$为$\Z_q$上的广义bent函数.
证明:由$(2,q)=1$得有$a\in\Z$使$2a\equiv1~(mod~q)$. 对于$y\in\Z_q,~W_f(y)=\displaystyle\sum_{x=0}^{q-1}\zeta_q^{x^2-xy}=\displaystyle\sum_{x=0}^{q-1}\zeta_q^{x^2-2axy}=\sum_{x=0}^{q-1}\zeta_q^{(x-ay)^2-a^2y^2}=\zeta_q^{-a^2y^2}\sum_{x=0}^{q-1}\zeta^{x^2}_q$.
而(利用特征的性质)$$
\begin{aligned}
|\sum_{x=0}^{q-1}\zeta_q^{x^2}|^2&=\sum_{x,z=0}^{q-1}\zeta_q^{x^2-z^2}=\sum_{x,z=0}^{q-1}\zeta_q^{(x+z)(x-z)}\\
&\overset{a=x+z,b=x-z}{=}\sum_{a,b=0}^{q-1}\zeta_q^{ab}=\sum_{\substack{a,b=0\\b=0}}^{q-1}\zeta_q^{ab}+\sum_{\substack{a,b=0\\b\neq0}}^{q-1}\zeta_q^{ab}\\
&=\sum_{a=0}^{q-1}1+\sum_{b=1}^{q-1}\sum_{a=0}^{q-1}\zeta_q^{ab}=q+0=q
\end{aligned}
$$ 于是$|W_f(y)|=|\sum_{x=0}^{q-1}\zeta_q^{x^2}|=q^\frac{1}{2}$,所以$f$是广义bent函数.
(2)$q=2^{2k}~(k\geq1)$
对每个整数$x,y,~0\leq x,y\leq q-1$,都可唯一表示为$x=2^k\cdot x_1+x_2,~y=2^ky_1+y_2,~0\leq x_1,x_2,y_1,y_2\leq2^k-1.$
引理3 设$q=2^{2k}~(k\geq1)$,定义$f:\Z_q\rarr\Z_q$为$f(x)=2^k\cdot x_1x_2$,则$f$为$\Z_q$上的广义bent函数.
证明:对于$y=2^ky_1+y_2,~0\leq y_1,y_2\leq 2^k-1$,则$$
\begin{aligned}
W_f(y)&=\sum_{x_1,x_2=0}^{2^k-1}\zeta_q^{2^kx_1x_2-(2^kx_1+x_2)(2^ky_1+y_2)}\\
&=\sum_{x_1,x_2=0}^{2^k-1}\zeta_q^{2^k(x_1x_2-x_1y_2-x_2y_1)-x_2y_2}\\
&=\sum_{x_2=0}^{2^k-1}\zeta_q^{-2^kx_2y_1-x_2y_2}\sum_{x_1=0}^{2^k-1}\zeta_q^{2^kx_1(x_2-y_2)}\\
&=2^k\sum_{\substack{x_2=0\\x_2=y_2}}^{2^k-1}\zeta_q^{-2^kx_2y_1-x_2y_2}=2^k\zeta_q^{-2^ky_1y_2-y_2^2}
\end{aligned}
$$ 因此$|W_f(y)|=2^k$,即$f$为广义bent函数.
(3)$q=2^{2k+1}~(k\geq1)$
每个整数$x(0\leq x\leq q-1)$均有二进制展开$$
x=\sum_{j=0}^{2k}x_j\cdot2^j~(x_j=0~or~1)
$$ 记$$
x^{(1)}=\sum_{j=0}^{k-1}x_j\cdot2^j,~x^{(2)}=x_k\cdot 2^k\\
x^{(3)}=\sum_{j=k+1}^{2k}x_j\cdot2^j=2^{k+1}\sum_{j=0}^{k-1}x_{j+k+1}\cdot2^j=2^{k+1}\ol{x}^{(3)}
$$ 于是$x=x^{(1)}+x^{(2)}+x^{(3)}$
引理4 设$q=2^{2k+1}~(k\geq1)$,定义$f:\Z_q\rarr\Z_q$为$f(x)=x^{(1)}x+2^{k-1}x^{(2)}$,则$f$为$\Z_q$上的广义bent函数.
证明:将$y~(0\leq y\leq q-1)$也表示为$y=y^{(1)}+y^{(2)}+y^{(3)}$. $$
\begin{aligned}
W_f(y)&=\sum_{x=0}^{q-1}\zeta_q^{f(x)-xy}\\
&=\sum^{2^k-1}_{x^{(1)},\ol{x}^{(3)}=0}\sum^1_{x_k=0}\zeta_q^{x^{(1)}(x^{(1)}+2^kx_k+2^{k+1}\ol{x}^{(3)})+2^{2k-1}x_k}\\
&\cdot\zeta_q^{-(x^{(1)}+2^kx_k+2^{k+1}\ol{x}^{(3)})(y^{(1)}+2^ky_k+2^{k+1}\ol{y}^{(3)})}\\
&=\sum_{x^{(1)},\ol{x}^{(3)}=0}^{2^k-1}\sum_{x_k=0}^1\zeta_q^{x^{(1)^2}+2^kx_kx^{(1)}+2^{k+1}x^{(1)}\ol{x}^{(3)}+2^{2k-1}x_k-x^{(1)}y^{(1)}}\\
&\cdot\zeta_q^{-2^k(x^{(1)}y_k+y^{(1)}x_k)-2^{k+1}(x^{(1)}\ol{y}^{(3)}+y^{(1)}\ol{x}^{(3)})-2^{2^k}x_ky_k}\\
&=\sum_{x^{(1)}=0}^{2^k-1}\zeta_q^{x^{(1)^2}-x^{(1)}(y^{(1)}+2^ky_k+2^{k+1}\ol{y}^{(3)})}\cdot\\
&\sum^1_{x_k=0}\zeta_q^{2^kx_k(x^{(1)}-y^{(1)}+2^{k-1}-2^ky_k)}\sum_{\ol{x}^{(3)}=0}^{2^k-1}\zeta_q^{2^k\ol{x}^{(3)}(x^{(1)}-y^{(1)})}\\
&=2^k\zeta_q^a\sum_{x_k=0}^1\zeta_q^{2^kx_k(2^{k-1}-2^ky_k)}\quad let ~a=-y^{(1)}(2^ky_k+2^{k+1}\ol{y}^{(3)})\\
&=2^k\zeta_q^a\sum_{x_k=0}^1\zeta_4^{x_k(1-2y_k)}=2^k\zeta_q^a(1\pm i)
\end{aligned}
$$ 因此$|W_f(y)|=2^{k+\frac12}$,即$f$为广义bent函数.
(4)$q=2^l\cdot r$,其中$l\geq2,2\not|r\geq3$. 每个整数$x(0\leq x\leq q-1)$可唯一表示为$$ x=2^lx_1+x_2,0\leq x_1<r, 0\leq x_2<2^l $$ 由$(2^{l-1},r)=1$知存在整数$e,f,~0\lt e\lt f,~0\lt f\lt2^{l-1}$使$2^{l-1}e-rf=1$.
引理 设$h:\Z_{2^l}\rarr\Z_{2^l}$是广义bent函数,令$g:\Z_{2^l}\rarr\Z_q$为函数$$
g(s)=rh(s)+2^{l-2}(r+1)^2e^2s^2\quad(0\leq s\leq 2^l-1)
$$ 则$f:\Z_q\rarr\Z_q,~f(x)=g(x_2)+2^l(x_1^2+ex_1x_2)$为广义bent函数
证明:对每个$y\in\Z_q$. $$
\begin{aligned}
W_f(y)&=\sum_{x_1=0}^{r-1}\sum_{x_2=0}^{2^l-1}\zeta_q^{g(x_2)+2^l(x_1^2+ex_1x_2)-(2^lx_1+x_2)y}\\
&=\sum_{x_2=0}^{2^l-1}\zeta_q^{g(x_2)-x_2y}\sum^{r-1}_{x_1=0}\zeta_r^{x_1^2+ex_1x_2-x_1y}
\end{aligned}
$$ 而$$
\begin{aligned}
&\sum_{x_1=0}^{r-1}\zeta_r^{x_1^2+(ex_2-y)x_1}=\sum_{x_1=0}^{r-1}\zeta_r^{(x_1+\frac{r+1}{2}(ex_2-y))^2-\frac{(r+1)^2}{4}(ex_2-y)^2}\\
&=\zeta_r^{-(\frac{r+1}{2})^2(ex_2-y)^2}\sum_{x_1=0}^{r-1}\zeta_r^{x_1^2}\quad(|\sum_{x_1=0}^{r-1}\zeta_r^{x_1^2}|=\sqrt{r})
\end{aligned}
$$ 则$$
\begin{aligned}
|W_f(y)|&=\sqrt{r}|\sum_{x_2=0}^{2^l-1}\zeta_q^{g(x_2)-x_2y}\cdot\zeta_r^{-(\frac{r+1}{2})^2(ex_2-y)^2}|\\
&=\sqrt{r}|\sum_{x_2=0}^{2^l-1}\zeta_q^{rh(x_2)+2^{l-2}(r+1)^2e^2x_2^2-x_2y-2^{l-2}(r+1)^2(e^2x_2^2-2ex_2y+y^2)}|\\
&=\sqrt{r}|\sum_{x_2=0}^{2^l-1}\zeta_q^{rh(x_2)+2^{l-1}(r+1)^2eyx_2-2^{l-2}(r+1)^2y^2-x_2y}|\\
&=\sqrt{r}|\sum_{x_2=0}^{2^l-1}\zeta_q^{rh(x_2)+(1+rf)(r+1)^2yx_2-x_2y}|\\
&=\sqrt{r}|\sum_{x_2=0}^{2^l-1}\zeta_{2^l}^{h(x_2)+cyx_2}|
\end{aligned}
$$ 其中$c=\frac{(1+rf)(r+1)^2-1}{r}\in\Z$,因为$h$是$\Z_{2^l}$上广义bent函数,则$|W_f(y)|=\sqrt{r}\sqrt{2^l}=\sqrt{q}$