$\gdef\lrb#1{\lbrace#1\rbrace}$ $\gdef\fpn{\mathbb{F}_{p^n}}$ $\gdef\F{\mathbb F}$
定义:设$f(x)$是$\F_q[x]$中n次首1不可约多项式,$f(x)\neq x$,如果$f(x)$的所有根均为$q^n-1$阶元素($\F_{q^n}$的本原元),则$f(x)$为$\F_q[x]$中的本原多项式.
设$\F^*_{q^n}=<\alpha>$,即$\alpha$是$\F_{q^n}$的一个本原元,则$\F^*_{q^n}$中元素为$\alpha^i(1\leq i\leq q^n-1)$.
由于$\alpha$的阶为$q^n-1$,则$\alpha^i$的阶为$\frac{q^n-1}{(i,q^n-1)}$.
因此:$\alpha^i$为本原元当且仅当$(i,q^n-1)=1$, 这表明$\F_{q^n}$中本原元共有$\varphi(q^n-1)$个,而每个n个本原元是$\F_{q}[x]$中一个n次本原多项式的根,所以$\F_q[x]$中n次本原多项式的个数为$\frac1n\varphi(q^n-1)$.
例1:对于$q=2,\F_2[x]$中4次首1不可约多项式的个数为$N_4=\frac14\sum_{d|4}\mu(d)q^\frac4d=\frac14(2^4-2^2)=3$.
由于$\F_2[x]$中1次首一不可约多项式为$x,x+1$,2次首一不可约多项式只有$x^2+x+1$,由此得出$\F_2[x]$中三个4次首1不可约多项式为$x^4+x+1,x^4+x^3+1,x^4+x^3+x^2+x+1$.
$\F_2[x]$中4次本原多项式的个数为$\frac14\varphi(2^4-1)=2$,而$x^4+x^3+1,x^4+x^3+x^2+x+1|x^5-1$,所以$x^4+x^3+1,x^4+x^3+x^2+x+1$的每个根都是5阶元素,$\F_{2^4}$中本原元的阶为15,所以$\F_{2^4}[x]$中4次本原多项式为$x^4+x+1,x^4+x^3+1$.
$x^{2^4}-x=x^{16}-x$为$\F_2[x]$中次数除尽4的所有首1不可约多项式之积,因此$x^{16}-x$在$\F_2[x]$中的分解为$$ x(x+1)(x^2+x+1)(x^4+x+1)(x^4+x^3+1)(x^4+x^3+1)(x^4+x^3+x^2+x+1) $$ 例2:在$\F_2[x]$中将$x^{60}-1$作因式分解. $x^{60}-1=(x^{20}-1)^3$,只需分解$f(x)=x^{20}-1$. $$ \begin{aligned} &f(x)=x^{20}-1=(x^{10}-1)(x^{10}+1)\\ &=(x^5-1)(x^5+1)(x^2+1)(x^8-x^6+x^4-x^2+1)\\ &=(x-1)(x+1)(x^4+x^3+x^2+x+1)(x^4-x^3+x^2-x+1)(x^2\\&+1)(x^8-x^6+x^4-x^2+1) \end{aligned} $$ (等比数列前n项和是一种方法)。可验证$x^4+x^3+x^2+1+1$和$x^4-x^3+x^2-x+1$不可约(求导互素),故只需分解$x^8-x^6+x^4-x^2+1$
对于$f(x)=x^{20}-1,f'(x)=20x=2x,(f(x),f'(x))=1$,因此$f(x)$没有重根,所以$f(x)$的20个根形成乘法群,即若$\alpha,\beta$为$x^{20}-1$的根,则$\alpha^{20}=\beta^{20}=1$,进而$(\alpha\alpha^{-1})^{20}=(\alpha^{-1})^{20}=1,(\alpha\beta)^{20}=1$,从而$\alpha\beta$和$\alpha^{-1}$也是$x^{20}-1$的根.
由于$x^{20}-1|x^{81}-x,x^{81}-x$的所有根形成$\F_3$的扩域$\F_{81}=\F_{3^4}$(定理13),所以$x^{20}-1$的所有根均在$\F^*_{81}$中,乘法群$\F^*_{81}$是80阶循环群,循环群的子群也是循环群,所以$x^{20}-1$的根形成20阶循环子群.
所以$x^{20}-1$必有一个阶为20的根$\alpha$,全部20个根为$\alpha^i(0\leq i\leq19)$.
对每个$\alpha^i,\alpha^i$在$\F_3$上的极小多项式$g(x)$是$x^{20}-1$在$\F_3[x]$上的一个首1不可约多项式因子.
由于$\alpha^i$为$g(x)$的根,从而$\alpha^{i\cdot3},\alpha^{i\cdot3^2},\cdots$也是$g(x)$的根(F_3上),以$l$表示满足$\alpha^{i\cdot3^l}=\alpha^i$的最小正整数.
由于$\alpha$的阶为20,$l$也是满足$i\cdot3^l\equiv i(mod~20)$的最小正整数. 因此$g(x)$的全部根为$\alpha^{i\cdot3^\lambda}(0\leq\lambda\leq l-1). g(x)$是$l$次不可约多项式.
例如对$i=2$,设$g(x)$为$\alpha^2$在$\F_3[x]$上的极小多项式,$g(x)$的根为$\alpha^2,\alpha^{3\cdot2}=\alpha^6,\alpha^{3\cdot6}=\alpha^{18},\alpha^{3\cdot18}=\alpha^{14}$,而$\alpha^{3\cdot14}=\alpha^2$,所以$g(x)$的全部根为$\alpha^2,\alpha^6,\alpha^{18},\alpha^{14}. g(x)$为4次首1不可约多项式.
对于$x^{20}-1$的20个根$\alpha^i(0\leq i\leq19)$,可按上述方法把同一个不可约多项式的根放在一起,得到
$\lrb{\alpha^0}=1$
$\lrb{\alpha,\alpha^3,\alpha^9,\alpha^7}(\alpha^{3\cdot7}=\alpha^{21}=\alpha)$
$\lrb{\alpha^2,\alpha^6,\alpha^{18},\alpha^{14}}(\alpha^{3\cdot14}=\alpha^2)$
$\lrb{\alpha^4,\alpha^{12},\alpha^{16},\alpha^8}$
$\lrb{\alpha^5,\alpha^{15}}$
$\lrb{\alpha^{10}=-1}$
$\lrb{\alpha^{11},\alpha^{13},\alpha^{19},\alpha^{17}}$
因此,$x^{20}-1$在$\F_3[x]$中是7个首一不可约多项式之积,分别是2个1次,1个2次,4个4次.
由之前$$
\begin{aligned}
&f(x)=(x-1)(x+1)(x^4+x^3+x^2+x+1)(x^4-x^3+x^2-x+1)(x^2\\&+1)(x^8-x^6+x^4-x^2+1)
\end{aligned}
$$ 可知$x^8-x^6+x^4-x^2+1$可分解为两个4次不可约多项式,设$x^8-x^6+x^4-x^2+1=g_1(x)g_2(x)$,其中$g_1(x)$和$g_2(x)$分别为$\F_3[x]$中的4次首一不可约多项式.
下面寻找$f(x)$分解式中不同多项式分别对应哪一组根
(1) $x^4+x^3+x^2+x+1=\frac{x^5-1}{x-1}$,则这个多项式的根为5阶元素$\lrb{\alpha^4,\alpha^{12},\alpha^{16},\alpha^8}$
(2) $x^4-x^3+x^2-x+1$可以整除$x^{10}-1$,但不能整除$x^5-1,x^5+1$,则这个多项式的根为10阶元素$\lrb{\alpha^2,\alpha^6,\alpha^{18},\alpha^{14}}$
对于$x^8-x^6+x^4-x^2+1=g_1(x)g_2(x)$,$g_1(x)$和$g_2(x)$的根为$\lrb{\alpha,\alpha^3,\alpha^9,\alpha^7}$和$\lrb{\alpha^{11},\alpha^{13},\alpha^{19},\alpha^{17}}$.
设$g_1(x)=x^4+ax^3+bx^2+cx+d=(x-\alpha)(x-\alpha^3)(x-\alpha^9)(x-\alpha^7)$,其中$a,b,c,d\in\F_3$,则$d=\alpha\alpha^3\alpha^9\alpha^7=\alpha^{20}=1$.
注意到$g_2(x)=(x-\alpha^{11})(x-\alpha^{13})(x-\alpha^{19})(x-\alpha^{17})$的4个根为$g_1(x)$的4个根的逆,则$$
\begin{aligned}
&g_2(x)=\alpha^{11+13+19+17}(\alpha^9x-1)(\alpha^7x-1)(\alpha x-1)(\alpha^3x-1)\\
&=x^4(x^{-1}-\alpha)(x^{-1}-\alpha^3)(x^{-1}-\alpha^9)(x^{-1}-\alpha^7)=x^4g_1(x^{-1})\\
&=x^4(x^{-4}+ax^{-3}+bx^{-2}+cx^{-1}+1)=x^4+cx^3+bx^2+ax+1
\end{aligned}
$$ 称为$g_1(x)$的反向多项式.
于是$x^8-x^6+x^4-x^2+1=(x^4+ax^3+bx^2+cx+1)(x^4+cx^3+bx^2+ax+1)$,比较$x^7$的系数,得$0=a+c$,从而$x^8-x^6+x^4-x^2+1=(x^4+bx^2+1)^2-a^2x^2(x^2-1)^2$.
比较$x^2$和$x^4$的系数,得到$\begin{cases}-1=2b-a^2\\1=2+b^2+2a^2\end{cases}$,在$\F_3$中方程组的解为$(a,b)=(\pm1,0)$,因此$x^8-x^6+x^4-x^2+1=(x^4+x^3-x+1)(x^4-x^3+x+1)$.
定义:$\F_q[x]$中多项式$f(x)$叫做是具有周期的,是指存在正整数$l$,使得$f(x)|x^l-1$. 满足此条件的最小正整数$l$叫做$f(x)$的周期,即为$per(f)$.
引理:设$f(x)$为$\F_q[x]$中具有周期的多项式,则对每个正整数$l$,$f(x)|x^l-1$当且仅当$per(f)|l$.
证明:若$per(f)|l$,则$x^{per(f)}-1|x^l-1$. 由于$f(x)|x^{per(f)}-1$,所以$f(x)|x^l-1$.
反之,若$f(x)|x^l-1$,用$per(f)$去除$l$,$l=q~per(f)+r,q,r\in\Z,0\leq r\leq per(f)-1$. 于是$f(x)|(x^{per(f)-1},x^l-1)=(x^{per(f)-1},x^l-1)=(x^{per(f)-1},x^r-1)$,故$f(x)|x^r-1$,从$0\leq r\leq per(f)-1$可知$r=0$,即$per(f)|l$.
对于$\F_q[x]$中n次首1不可约多项式$f(x),f(x)\neq x$,则$f(x)|x^{q^n-1}-1$(定理17),因此$f(x)$的周期是$q^n-1$的因子.
并且$f(x)$的周期是$q^n-1$当且仅当$f(x)$为本原多项式.
定理:设$f(x)\in\F_q[x],f(0)\neq0$(即$x\not|f(x)$),$deg~f(x)\geq1,q=p^m,$其中$p$为素数,$m\geq1$,则
(1) 若$f(x)$是$\F_q[x]$中不可约多项式,则$per(f)$为$f(x)$中每个根的阶,并且$per(f)|q^{deg~f(x)}-1$.
(2) 若$f(x)=g(x)^b,$其中$g(x)$是$\F_q[x]$中不可约多项式,$b\geq1.$ 令$t$是满足$p^t\geq b$的最小正整数,则$per(f)=p^t\cdot per(g)$.
证明:记$e=per(g)$,由$g(x)|x^e-1$和$b\leq p^t$可知$f(x)=g(x)^b|g(x)^{p^t}|(x^e-1)^{p^t}=x^{ep^t}-1$. 所以$per(f)|ep^t$.
另一方面,记$d=deg~g(x)$,则$e|q^d-1$,从而$(e,p)=1$,由$g(x)|f(x)$可知$g(x)|x^{per(f)}-1$,于是$e=per(g)|per(f)|ep^t$. 这表明$per(f)=ep^l$,其中$l\leq t$. 因此$f(x)=g(x)^b|x^{ep^l}-1=(x^e-1)^{p^l}$. 由于$g(x)$和$x^e-1$都没有重根,则$b\leq p^l$. 由$t$的定义知道$l\geq t$,所以$per(f)=ep^t$.
(3) 设$f(x)=f_1(x)f_2(x)\cdots f_s(x)$,其中$f_1(x),f_2(x),\cdots,f_s(x)$是$\F_q[x]$中彼此互素的多项式,$deg~f_i(x)\geq1(1\leq i\leq s)$则$per(f)=[per(f_1),per(f_2),\cdots,per(f_s)]$.
证明:由于$f(x)=f_1(x)f_2(x)\cdots f_s(x)$两两互素,则对每个正整数n,$$
\begin{aligned}
f(x)|x^n-1\lrArr f_i(x)|x^n-1(1\leq i\leq s)\\
\lrArr per(f_i)|n(1\leq i\leq s)\\
\lrArr [per(f_1),per(f_2),\cdots,per(f_s)]|n
\end{aligned}
$$ 于是$per(f)=[per(f_1),per(f_2),\cdots,per(f_s)]$.
例:求$\F_2[x]$中多项式$f(x)=(x^2+x+1)^3(x^4+x+1)$的周期
解:$x^2+x+1|x^3-1$是$\F_2[x]$中不可约多项式,周期为3. $x^4+x+1$是$\F_2[x]$本原多项式,周期为$2^4-1=15$. $(x^2+x+1)^3$的周期为$3\cdot2^2=12$,于是$f(x)$的周期为$[12,15]=60$.
有限域上的幂级数环
幂级数环表示为$R=\F_q[[x]]$.
通信中的信息对应数学序列$$
\alpha=(a_0,a_1,\cdots,a_n,\cdots)(a_i\in\F_q)
$$ 对应于环$R$中的一个幂级数$$
\alpha(x)=a_0+a_1x+\cdots+a_nx^n+\cdots=\sum_{n=0}^\infty a_nx^n\in R
$$ 幂级数的加法和乘法对应于序列的运算.
多项式环$\F_q[x]$是$R=\F_q[[x]]$的子环.
设$f(x)\in\F_q[x],f(0)\neq0$,则$f(x)$是$R=\F_q[[x]]$中可逆元素,于是对每个$g(x)\in\F_q[x]$,有理函数$a(x)=\frac{f(x)}{g(x)}\in R$,即$a(x)$可展开成幂级数.
类似于有理数是循环小数,可以证明:上述有理函数作为幂级数,它所对应的q元序列是周期序列.
定义:q元序列$\alpha=(a_0,a_1,\cdots,a_n,\cdots)(a_i\in\F_q)$叫做是周期序列,是指存在$N\geq0,l\geq1$使得$a_{n+l}=a_n(n\geq N)$
满足此条件的最小正整数$l$叫做该序列的周期,这个周期序列也记为$\alpha=(a_0a_1\cdots a_{N-1}\dot{a}_Na_{N+1}\cdots\dot{a}_{N+l-1})$,其中$a_Na_{N+1}\cdots a_{N+l-1}$叫做它的一个周期节.
当$N=0$时,此序列叫做是纯周期序列,表示成$\alpha=(\dot{a}_0a_1\cdots\dot{a}_{l-1})$.
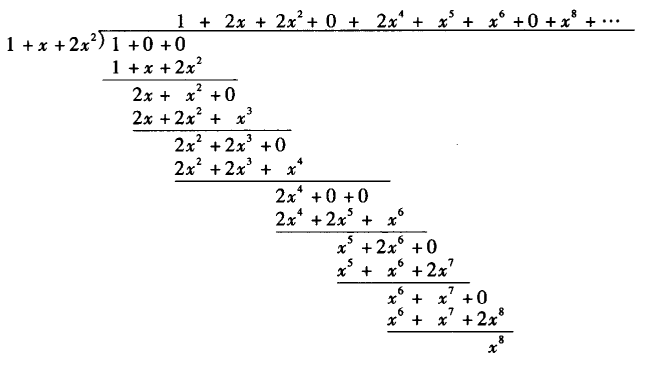
例如:多项式$1+x+2x^2$在$\F_3[[x]]$中可逆,我们可以按升幂的方式用$1+x+2x^2$去除1得到$(1+x+2x^2)^{-1}$的幂级数形式.


比如:对每个正整数$n,(1-x^n)^{-1}=1+x^n+x^{2n}+\cdots,$它对应于周期为n的序列$(\dot10\cdots\dot0)$
一般的,对每个多项式$g(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}$,$\frac{g(x)}{1-x^n}=(\dot{a}_0a_1\cdots\dot{a}_{n-1})$
定理:(1)q元周期序列$\alpha$和有理函数$\frac{g(x)}{f(x)}(f(x),g(x)\in\F_q[x],f(0)\neq0)$一一对应,并且:$\alpha$是纯周期序列当且仅当对应的$\frac{g(x)}{f(x)}$是真分式(即$deg~g(x)<deg~f(x)$).
(2)若$\frac{g(x)}{f(x)}$是即约分式,(即$(f(x),g(x))=1$),则对应序列的周期等于多项式$f(x)$的周期.
例:考虑$\alpha(x)=\frac{1+x^2}{1+x+x^3+x^5}\in\F_2[x]$对应的二元序列.
由$(1+x^2,1+x+x^3+x^5)=1+x,\alpha(x)$化为既约真分式$\frac{1+x}{1+x^3+x^4}$,对应二元序列$\alpha$是纯周期序列,$\alpha$的周期等于多项式$1+x^3+x^4$的周期15. 所以只需求出该序列的前15位,可用除法算式得出,也可以求出$\frac{1-x^{15}}{1+x^3+x^4}=h(x)\in\F_2[x]$,则前15位即为$(1+x)h(x)$的系数. 还可用下面的引理递推算出.
引理:设$h(x)=1+c_1x+\cdots+c_nx^n,g(x)=b_0+b_1x+\cdots+b_{n-1}x^{n-1}$是$\F_q[x]$中多项式,$c_n\neq0$,则$\frac{g(x)}{f(x)}$对应的q元序列$\alpha=(a_0,a_1,\cdots,a_n,\cdots)$,可如下递推求出$$ \begin{aligned} a_0=b_0,a_1=b_1-a_0c_1,\cdots,a_{n-1}=b_{n-1}-(a_{n-2}c_1+\cdots+a_0c_{n-1}),\\ a_{n+i}=-(a_{n+i-1}c_1+a_{n+i-2}c_2+\cdots+a_ic_n)(i=0,1,2,\cdots) \end{aligned} $$
有限域的加法特征和乘法特征
定义:有限域$\F_q$加法群的特征叫做$\F_q$的加法特征,是指加法群$\F_q$到乘法群$C^*$的同态$\lambda:\F_q\rarr C^*$,即$\lambda(a+b)=\lambda(a)\lambda(b)$.
乘法群$\F^*_q$的特征叫做是$\F_q$的乘法特征,是指乘法群的同态$\chi:\F^*_q\rarr C^*$,即$\chi(ab)=\chi(a)\chi(b)$.
乘法群$\F^*_q$是$q-1$阶循环群,即$\F^*_q=<\alpha>=\lrb{1,\alpha,\alpha^2,\cdots,\alpha^{q-2}}$,其中$\alpha$是$\F_q$的本原元,每个乘法特征$\chi$由它在$\alpha$处的取值$\chi(\alpha)$完全确定.
$1=\chi(\alpha^{q-1})=\chi(\alpha)^{q-1}$,则$\chi(\alpha)=\zeta^i_{q-1}(1\leq i\leq q-2)$,其中$\zeta_{q-1}=e^\frac{2\pi i}{q-1}$.
用$\chi$表示$\chi(\alpha)=\zeta_{q-1}$的乘法特征,那么$\F_q$的全部特征为$\lrb{\chi^i:0\leq i\leq q-1}$($\chi^{q-1}=\chi^0$是平凡特征)
所以$\F_q$的乘法特征形成$q-1$阶循环群(同构于乘法群$\F_q^*$).
另一方面,$\F_q$是$\F_p$上的m维向量空间$(q=p^m)$. 所以$\F_q$的加法群是$m$个$\F_p$的直和,而每个$\F_p$是p阶循环群.
所以$\F_q$的加法特征群也是m个p阶循环群的直积.
即$\F_q$中的一组$\F_p$基$u_1,u_2,\cdots,u_m,\F_q$中元素可表示为向量$a=a_1u_1+a_2u_2+\cdots+a_mu_m=(a_1,a_2,\cdots,a_m)(a_i\in\F_q)$.
定理:对每个$b=(b_1,b_2,\cdots,b_m)(b_i\in\F_q)$,映射$\lambda_b:\F_q\rarr C^*,\lambda_b(a)=\zeta_p^{a_1b_1+a_2b_2+\cdots+a_mb_m}(\zeta_p=e^\frac{2\pi i}{q-1})$是$\F_q$的加法特征,当$b$跑过全部向量时,$\lambda_b$给出全部$p^m$个不同的加法特征,并且$\lambda_b\cdot\lambda_{b'}=\lambda_{b+b'}$.
证明:只需证当$b\neq b'$时,$\lambda_b\neq\lambda_{b'}$
由于$\lambda_b\cdot\lambda_{b'}^{-1}=\lambda_{b-b'}$,所以只需证明当$b\neq0$时$\lambda_b$不是平凡特征.
由于$b=(b_1,b_2,\cdots,b_m)\neq0$,可知存在$i$使得$b_i\neq0$,于是对$a=(0,\cdots,0,1,0,\cdots,0)$(第i个分量为1),则$\lambda_b(a)=\zeta^{b^i}_p\neq1$,即$\lambda_b$不是平凡特征.
下面给出$\F_q$的加法特征的另一种刻画方式
定理:记$G=G(\F_{q^n}/\F_q)=<\tau>$表示有限域n次扩张$\F_{q^n}/\F_q$的伽罗瓦群,它是由$\tau$生成的n阶循环群,其中$\tau(\alpha)=\alpha^q$,则
(1) $T:\F_{q^n}\rarr\F_q,T(\alpha)=\sum_{\sigma\in G}\sigma(\alpha)=\tau(\alpha)+\tau^2(\alpha)+\cdots+\tau^n(\alpha)=\alpha+\alpha^q+\cdots+\alpha^{q^{n-1}}$是加法群的满同态.
证明:证明$T$的像在$\F_q$中,由于$T(\alpha)^q=(\alpha+\alpha^q+\cdots+\alpha^{q^{n-1}})^q=\alpha^q+\alpha^{q^2}+\cdots+\alpha^{q^{n-1}}+\alpha=T(\alpha)\in\F_q$. 容易证明$T(\alpha+\beta)=T(\alpha)+T(\beta)$.
所以$T$是加法群同态,进而$Ker(T)$中元素为多项式$x^{q^{n-1}}+x^{q^{n-2}}+\cdots+x^q+x$的根,所以$|Ker(T)|\leq q^{n-1}$. 于是$q=|\F_q|\geq|Im(T)|=\frac{|\F_{q^n}|}{|Ker(T)|}\geq\frac{q^n}{q^{n-1}}=q$,则$|Im(T)|=q$,即$T$是满同态.
(2) $T$是$\F_q$线性映射,即对$a\in\F_q,\alpha\in\F_{q^n},T(a\alpha)=aT(\alpha)$.
证明:当$a\in\F_q,\alpha\in\F_{q^n}$时$T(a\alpha)=a\alpha+(a\alpha)^q+\cdots+(a\alpha)^{q^{n-1}}=a\alpha+a\alpha^q+\cdots+a\alpha^{q^{n-1}}=aT(\alpha)$.
定义:上面的映射$T$叫做有限域扩张$F_{q^n}/\F_q$的迹映射,表示成$T_{\F_{q^n}/\F_q}$
定理:设$q=p^m$,$T$是从$\F_q$到$\F_p$的迹映射,则对每个$\beta\in\F_q$,映射$\lambda_\beta:\F_q\rarr C^*,\lambda_\beta(\alpha)=\zeta^{T(\alpha\beta)}_p(\alpha\in\F_q)$是$\F_q$的加法特征,并且$\lambda_\beta$给出$\F_q$的全部q个加法特征,进而$\lambda_\beta\cdot\lambda_{\beta'}=\lambda_{\beta+\beta'}$.
$\F_q$上纯周期序列对应真分式$\frac{g(x)}{f(x)}$
$\F_q$上纯周期序列对应真分式$\frac{g(x)}{f(x)}(f(x),g(x)\in\F_q[x])$,$\F_q$上纯周期序列还可以表示成迹表达式.
定理:设$f(x)$是$\F_q[x]$中的n次多项式,$n\geq1$.
(1) 若$f(x)=f_1(x)f_2(x)\cdots f_s(x)$,其中$f_1(x),f_2(x),\cdots,f_s(x)$是$\F_q[x]$中彼此互素的多项式,则每个真分式$\frac{g(x)}{f(x)}(g(x)\in\F_q[x],deg~g(x)<n)$,都可唯一表达成$$
\frac{g(x)}{f(x)}=\frac{g_1(x)}{f_1(x)}+\frac{g_2(x)}{f_2(x)}+\cdots+\frac{g_s(x)}{f_s(x)}
$$ 其中$\frac{g_i(x)}{f_i(x)}(1\leq i\leq s)$都是真分式$(g_i(x)\in\F_q[x]),deg~g_i(x)<deg~f_i(x))$
(2) 若$f(x)=p_1(x)^{e_1}p_2(x)^{e_2}\cdots p_s(x)^{e_s}$是首1多项式$f(x)$在环$\F_q[x]$中的标准分解式,其中$p_1(x),p_2(x),...,p_s(x)$是$\F_q[x]$中彼此不同的首1不可约多项式($e_i\geq1(1\leq i\leq s)$),则每个真分式$\frac{g(x)}{f(x)}$可唯一表示成如下部分分式展开$$
\frac{g(x)}{f(x)}=\sum^s_{i=1}(\frac{a_{i,1}(x)}{p_i(x)}+\frac{a_{i,2}(x)}{p_i^2(x)}+\cdots+\frac{a_{i,e_i}(x)}{p_i^{e^i}(x)})
$$ 其中对每个$i(1\leq i\leq s), a_{i,j}(x)\in\F_q[x],deg~a_{i,j}(x)<deg~p_i(x)(1\leq j\leq e_i)$.
例:设$f(x)=(x^2+x+1)^2(x^3+x+1)\in\F_2[x]$,将$\frac{x^6+x^3+x^2+1}{f(x)}$作部分分式展开.
解:$x^2+x+1$和$x^3+x+1$是$\F_2[x]$中不可约多项式,则$\frac{x^6+x^3+x^2+1}{f(x)}=\frac{ax^3+bx^2+cx+d}{(x^2+x+1)^2}+\frac{ex^2+hx+l}{x^3+x+1}(a,b,c,d,e,h,l\in\F_2)$
即$x^6+x^3+x^2+1=(ax^3+bx^2+cx+d)(x^3+x+1)+(ex^2+hx+l)(x^4+x^2+1)$
比较系数得$$
\begin{cases}
a+e=1\\
b+h=0\\
a+c+l+e=0\\
a+b+d+h=1\\
b+c+l+e=1\\
c+d+h=0\\
d+l=1
\end{cases}
$$ 解出$b=c=d=e=h=0,a=l=1$,则$\frac{x^6+x^3+x^2+1}{f(x)}=\frac{x^3}{(x^2+x+1)^2}+\frac{1}{x^2+x+1}=\frac{x+1}{x^2+x+1}+\frac1{(x^2+x+1)^2}+\frac{1}{x^3+x+1}$
法2:求$\alpha(x),\beta(x)\in\F_2[x]$使得$x^6+x^3+x^2+1=\alpha(x)(x^3+x+1)+\beta(x)(x^2+x+1)^2$.
模$x^3+x+1$得$x^6+x^3+x^2+1\equiv\beta(x)(x^2+x+1)(mod~x^3+x+1)$
$$
\begin{aligned}
\beta(x)&\equiv\frac{x^6+x^3+x^2+1}{(x^2+x+1)^2}\equiv\frac{x+1}{(x^2+x+1)^2}(mod~x^3+x+1)\\
&\equiv\frac{x+1}{(x^3+x^2)^2}\equiv\frac{1}{x^4(x+1)}\equiv\frac{x^3+x}{x^4(x+1)}\\
&\equiv\frac{x+1}{x^3}\equiv\frac{x+1}{x+1}\equiv1(mod~x^3+x+1)
\end{aligned}
$$ 得$\beta(x)\equiv1,\alpha(x)(x^3+x+1)=x^6+x^3+x^2+1+(x^2+x+1)^2=x^6+x^4+x^3$,得$\alpha(x)=x^3$
在$\F_2[x]$中$\frac{x+1}{(x^2+x+1)^2}\equiv\frac{x+1}{(x^2+x^3)^2}~mod~(x^3+x+1)$
因为$x^3\equiv-(x+1)~mod~x^3+x+1\equiv x+1~mod~x^3+x+1$
定理(周期序列的迹表达式)
设$f(x)\in\F_q[x],f(0)\neq0,deg~f(x)\geq1$
(1) 若$f(x)$为$\F_q[x]$中n次不可约多项式,$\alpha$是$f(x)$在$\F_{q^n}$中的一个根,$\gamma=\alpha^{-1}$则对每个真分式$\frac{g(x)}{f(x)}$对应的$\F_q$上的纯周期序列$\frac{g(x)}{f(x)}=\sum^\infty_{k=0}a_kx^k(a_k\in\F_q)$,存在由$g(x)(g(x)\in\F_q[x],deg~g(x)<n)$唯一决定的$\beta\in\F_{q^n}$,使得$a_k=T_{\F_{q^n}/\F_q}(\beta\gamma^k)(k=0,1,2,...)$
证明:$\F_q(\alpha)=\F_{q^n}$,且$f(x)$有n个不同根$\alpha,\alpha^q,\alpha^{q^n-1}\in\F_{q^n}$
不妨设$f(0)=1$ $$
\begin{aligned}
f(x)&=\prod^{n-1}_{i=0}(\alpha^{q^i}-x)=\prod^{n-1}_{i=0}\alpha^{q^i}(1-\gamma^{q^i}x)\\
&=\alpha^\frac{1-q^n}{1-q}\prod^{n-1}_{i=0}(1-\gamma^{q^i}x)=\prod^{n-1}_{i=0}(1-\gamma^{q^i}x)
\end{aligned}
$$ 将$\frac{g(x)}{f(x)}$看成是$\F_{q^n}[x]$中的分式,由部分分式展开$$
\frac{g(x)}{f(x)}=\sum^{n-1}_{i=0}\frac{\beta_i}{1-\gamma^{q^i}x}=\frac{\beta_0}{1-\gamma x}+\frac{\beta_1}{1-\gamma^qx}+\cdots+\frac{\beta_{n-1}}{1-\gamma^{q^{n-1}}x}(\beta_i\in\F_{q^n})
$$
将域$\F_{q^n}$的$\F_q$自同构$\tau(\alpha)=\alpha^q(\alpha\in\F_{q^n})$作用于上式,而$g(x)$和$f(x)$的系数均属于$\F_q$,则$$
\frac{g(x)}{f(x)}=\sum^{n-1}_{i=0}\frac{\beta^q_i}{1-\gamma^{q_{i+1}}x}=\frac{\beta^q_0}{1-\gamma^{q}x}+\frac{\beta^q_1}{1-\gamma^{q_{2}}x}+\cdots+\frac{\beta^q_{n-2}}{1-\gamma^{q_{n-1}}x}+\frac{\beta^q_{n-1}}{1-\gamma x}
$$ 部分分式展开是唯一的,则$\beta_i=\beta^q_{i-1}(1\leq i\leq n-1),\beta^q_{n-1}=\beta_0$.
令$\beta_0=\beta$,则$$
\begin{aligned}
\frac{g(x)}{f(x)}&=\frac{\beta}{1-\gamma x}+\frac{\beta^q}{1-\gamma^qx}+\cdots+\frac{\beta^{q^{n-1}}}{1-\gamma^{q^{n-1}}x}=\sum^{n-1}_{i=0}\frac{\beta^{q^i}}{1-\gamma^{q^i}x}\\
&=\sum^{n-1}_{i=0}\beta^{q^i}\sum^\infty_{k=0}\gamma^{kqi}x^k=\sum^\infty_{k=0}x^k\sum^{n-1}_{i=0}\beta^{q^i}\gamma^{kqi}\\
&=\sum^\infty_{k=0}x^kT_{\F_{q^n}/F_q}(\beta\gamma^k)
\end{aligned}
$$ 于是对每个$k\geq0,a_k=T_{\F_{q^n}/F_q},\beta$由$g(x)$唯一决定.
(2) 若$f(x)=f_1(x)f_2(x)\cdots f_s(x)$,其中$f_i(x)(1\leq i\leq s)$是$\F_q[x]$中彼此互素的不可约多项式. $deg~f_i(x)=n_i,\alpha^i$为$f_i(x)$在$\F_{q^{n_i}}$中的一个根$\gamma_i=\alpha^{-1}_i(1\leq i\leq s)$,则对每个真分式$\frac{g(x)}{f(x)}$对应的$\F_q$上纯周期序列,存在由$g(x)$唯一决定的一组元素$\beta_i\in\F_{q^{n_i}}(1\leq i\leq s)$. 使$a_n=\sum^s_{i=1}T_{\F_{q^{n_i}}/\F_q}(\beta_i\gamma^i)(n=0,1,2,\cdots)$