Ch2 Syntax

2.1 Terminology

The syntax of a programming language determines the well-formed or grammatically correct programs of the language. Semantics describes how or whether such programs will execute.

• Syntax is how programs look
• Semantics is how programs work

A terminal or token is a symbol in the language.

• C++, Java, and Python terminals: while, for, (, ;, 5, b
• Type names like int and string

Keywords, types, operators, numbers, identifiers, etc. are all tokens or terminals in a language.

A syntactic category or nonterminal is a set of pharses, or strings of tokens, that will be defined in terms of symbols in the language (terminal and nonterminal symbols).

• C++, Java, or Python nonterminals: <statement>, <expression>, <if-statement>, etc.
• Syntactic categories define parts of a program like statements, expressions, declarations, and so on.

A metelanguage is a higher-level language used to specify, discuss, describe, or analyze another language.

2.2 Backus Naur Form (BNF)

Backus Naur Format (i.e. BNF) is a formal metalanguage for describing language syntax. BNF consists of a set of rules that have this form:

<syntactic category> ::= a string of terminals and nonterminals

The symbol ::= can be read as is composed of and means the syntactic category is the set of all items that correspond to the right hand side of the rule. Multiple rules defining the same syntactic category may be abbreviated using the | character which can be read as "or" and means set union.

2.2.1 BNF Examples (Java)

<method-declaration> ::=
    <modifiers> <type-specifier> <method declarator> <throws-clause> <method-body> |
    <modifiers> <type-specifier> <method declarator> <method-body> |
    <type-specifier> <method declarator> <throws-clause> <method-body> |
    <type-specifier> <method declarator> <method-body>

The set of method declarations is the union of the sets of method declarations that explicitly throw an exception with those that don't explicitly throw an exception with or without modifiers attached to their definitions.

2.2.2 Extended BNF (EBNF)

1. item? or [item] means the item is optional.
2. item* or {item} means zero or more occurrences of an item are allowable.
3. item+ means one or more occurrences of an item are allowable.
4. Parentheses may be used for grouping.

2.3 Context-Free Grammars

Most grammars are context-free, meaning that the contents of any syntactic category in a sentence are not dependent on the context in which it is used. A context-free grammar is defined as a four tuple:
$G=(\mathcal{N},\mathcal{T},\mathcal{P},\mathcal{S})$ where

• $\mathcal{N}$ is a set of symbols called nonterminals or syntactic categories.
• $\mathcal{T}$ is a set of symbols called terminals or token.
• $\mathcal{P}$ is a set of productions of the form $n\rarr\alpha$ where $n\in\mathcal{N}$ and $\alpha\in\{\mathcal{N}\cup\mathcal{T}\}^*$.
• $\mathcal{S}\in\mathcal{N}$ is a special nonterminal called the start symbol of the grammar.

2.3.1 The Infix Expression Grammar

A context-free grammar for infix expressions can be specified as $G=(\mathcal{N},\mathcal{T},\mathcal{P},E)$ where
$\mathcal{N}=\{E,T,F\}$
$\mathcal{T}=\{identifier, number, +, -, *, /, (, )\}$
$\mathcal{P}$ is defined by the set of productions $\begin{aligned} &E\rarr E~+~T~|~E~-~T~|~T\\ &T\rarr T~*~F~|~T~/~F~|~F\\ &F\rarr (E)|identifier|number \end{aligned}$

2.4 Derivation

A sentence of a grammar is a string of tokens from the grammar if it can be derived from the grammar. This process is called constructing a derivation. A derivation is a sequence of sentential forms that starts with the start symbol of the grammar and ends with the sentence you are trying to derive. A sentential form is a string of terminals, $\beta$, where $A\rarr\beta$ is a production in the grammar. For a grammar, G, the language of G is the set of sentences that can be derived from G and is usually written as L(G).

2.4.1 A Derivation

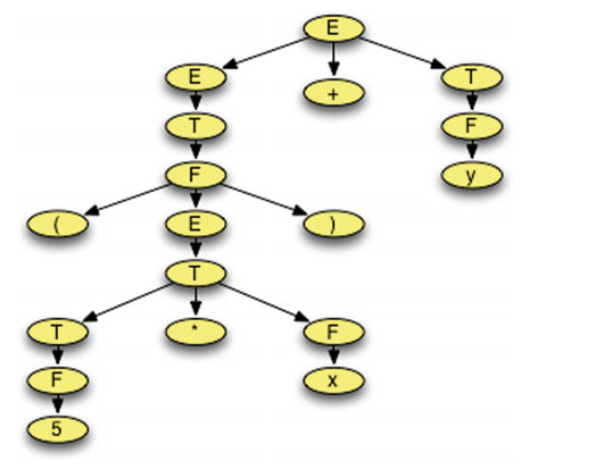
Here we prove that the expression (5*x)+y is a member of the language defined by the grammar given in Sect.2.3.1.

$\underline{E}\rArr\underline{E}+T\rArr\underline{T}+T\rArr\underline{F}+T\rArr(\underline{E})+T\rArr(\underline{T})+T\rArr(\underline{T}*F)+T\rArr(\underline{F}*F)+T\rArr(5*\underline{F})+T\rArr(5*x)+\underline{T}\rArr(5*x)+\underline{F}\rArr(5*x)+y$

Practice 2.1 Construct a derivation for the infix expression 4+(a-b)*x
$E\rArr E+T\rArr T+T\rArr F+T\rArr 4+T\rArr 4+T*F\rArr 4+F*F\rArr 4+(E)*x\rArr 4+(E-T)*x\rArr 4+(T-T)*x\rArr 4+(F-F)*x\rArr 4+(a-b)*x$

2.4.2 Types of Derivation

A sentence of a grammar is valid if there exists at least one derivation for it using the grammar.

• Left-most derivation - Always replace the left-most nonterminal when going from one sentential form to the next in a derivaiton.
• Right-most derivation - Always replace the right-most nonterminal when going from one sentential form to the next in a derivaiton.

Practice 2.2 Construct a right-most derivation for the expression x*y+z

$E\rArr E+T\rArr E+F\rArr E+z\rArr T+z\rArr T*F+z\rArr T*y+z\rArr F*y+z\rArr x*y+z$

2.4.4 The Prefix Expression Grammar

A context-free grammar for prefix expression can be specified as $G=(\mathcal{N},\mathcal{T},\mathcal{P},E)$ where
$\mathcal{N}={E}$
$\mathcal{T}=\{identifier,number,+,-,*,/\}$
$\mathcal{P}$ is defined by the set of productions$E\rarr +~E~E~|~-E~E~|~*E~E~|~/~E~E~|~identifier~|~number$

Practice 2.3 Construct a left-most derivation for the prefix expression +4*-abx.

$E\rArr+EE\rArr+4E\rArr+4*EE\rArr+4*-EEE\rArr+4*-abx$

2.5 Parse Trees

A grammar, G, can be used to build a tree representing a sentence of L(G). This kind of tree is called a parse tree. A grammar is ambiguous if and only if there is a sentence in the language of the grammar that has more than one parse tree.

2.6 Abstract Syntax Trees

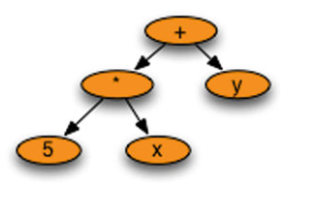
An abstract syntax tree is like a parse tree except that non-essential information is removed. More specifically,

• Nonterminal nodes in the tree are replaced by nodes that reflect the part of the sentence they represent.
• Unit productions in the tree are collapsed.

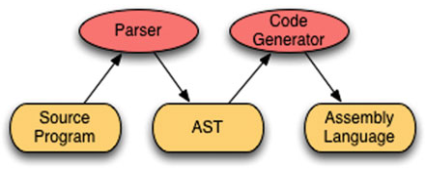
ASTs are used by compilers while generating code and may be used by interpreters when running your program. ASTs throw away superfluous information and retain only what is essential to allow a compiler to generate code or an interpreter to execute the program.

2.7 Lexical Analysis

The parser reads the tokens, or terminals, of a program and uses the language's grammar to check to see if the stream of tokens form a syntactically valid program. The tokenizer, or scanner, or lexer forms tokens from the individual characters of a source file. The tokens of a language can be described by another language called the language of regular expressions.

2.7.1 The Language of Regular Expressions

The context-free grammar of regular expressions is $RE=(\mathcal{N},\mathcal{T},\mathcal{P},E)$ where
$\mathcal{N}=\{E,T,K,F\}$
$\mathcal{T}=\{character,*,+,.,(,)\}$
$\mathcal{P}$ is defined by the set of productions
$E\rarr E+T|T$
$T\rarr T.K|K$
$K\rarr F*|F$
$F\rarr character|(E)$

The + operator is the choice operator, meaning either E or T, but not both. The dot operator means that T is followed by K. The * operator, called Kleene Star, means zeros or more occurrences of F. The grammar defines the precedence of these operators. At its most primitive level, a regular expression may be just a single character.

letter abbreviate A+B+...+Z+a+b+...+z and digit abbreviate 0+1+2+...+9.

Infix grammar: letter.letter*+digit.digit*+'+'+'-'+'*'+'/'+'('+')'

2.7.2 Finite State Machines

A finite state machine is a mathematical model that accepts or rejects strings of characters for some regular expression. A finite state machine is often called a finite state automation. Every regular expression has at least one finite state machine and vice versa, every finite state machine has at least one matching regular expression.

Formally a finite state automation is defined as follows.

$M=(\sum,S,F,s_0,\delta)$ where $\sum$ is the input alphabet (the character understood by the machine), $S$ is a set of states, $F$ is a subset of $S$ usually written as $F\subseteq S$, $s_0$ is a special state called the start state, and $\delta$ is a function that takes as input an alphabet symbol and a state and returns a new state. $\delta:\sum\times S\rarr S$.

The machine starts in the start state and reads characters one at a time. As characters are read, the finite state machine changes state. After reading all the characters of a token, if the current state is in the set of final states, F, then the token is accepted by the finite state machine.

2.7.3 Lexer Generators

To use a lexer generator you must write regular expressions for the tokens of the language and provide these to the lexer generator. A lexer generator will generate a lexer program that internally uses a finite state machine. (lex,flex...)

2.8 Parsing

Parsing is the process of detecting whether a given string of tokens is a valid sentence of a grammar.

• A top-down parser starts with the root of the parse tree.
• A bottom-up parse starts with the leaves of the parse tree.

Top-down and bottom-up parsers check to see if a sentence belongs to a grammar by constructing a derivation for the sentence, using the grammar. A parser either reports success (and possibly returns an abstract syntax tree) or reports failure (hopefully with a nice error message).

2.9 Top-Down Parsers

A top-down parser operates by (possibly) looking at the next token in the source file and deciding what to do based on the token and where it is in the derivation. To operate correctly, a top-down parser must be designed using a special kind of grammar called an LL(1) grammar. An LL(1) grammar is simply a grammar where the next choice in a left-most derivation can be deterministically chosen based on the current sentential form and the next token in the input. The first L refers to scanning the input from left to right. The second L signifies that while performing a left-most derivation, there is only 1 symbol of lookahead that is needed to make the decision about which production to choose next in the derivation.

Left recursive rules are not allowed in LL(1) grammars. A left recursive rule can be eliminated in a grammar through a straightforward transformation of its production. Common prefixes in the right hand side of two productions for the same nonterminal are also not allowed in an LL(1) grammar.

2.9.3 An LL(1) Infix Expression Grammar

$G=(\mathcal{N},\mathcal{T},\mathcal{P},E)$ where
$\mathcal{N}=\{E,RestE,T,RestT,F\}$
$\mathcal{T}=\{identifier,number,+,-,*,/,(,)\}$
$\mathcal{P}$ is defined by the set of productions$\begin{aligned} &E\rarr T~RestE\\ &RestE\rarr+T~RestE~|~-T~RestE~|~\varepsilon\\ &T\rarr F~RestT\\ &RestT\rarr*~F~RestT~|~/~F~RestT~|~\varepsilon\\ &F\rarr(E)~|~identifier~|~number \end{aligned}$ In this grammar the $\varepsilon$ is a special symbol that denotes an empty production.

2.10 Bottom-Up Parsers

In fact, most grammars for programming languages are LALR(1). The LA stands for look ahead with the 1 meaning just one symbol of look ahead. The LR refers to scanning the input from left to right while constructing a right-most derivation. A bottom-up parser constructs a right-most derivation of a source program in reverse. So, an LALR(1) parser constructs a reverse right-most derivation of a program.

Building a bottom-up parser is a somewhat complex task involving the computation of item sets, look ahead sets, a finite state machine, and a stack. The finite state machine and stack together are called a pushdown automaton. The construction of the pushdown automaton and the look ahead sets are calculated from the grammar.

A parser generator is a program that is given a grammar and builds a parser for the language of the grammar by constructing the pushdown automaton and lookahead sets needed to parse programs in the language of the grammar.

The original parser generator for Unix was called yacc, which stood for yet another compiler compiler since it was a compiler for grammars that produced a parser for a language. Since a parser is part of a compiler, yacc was a compiler compiler. The Linux version of yacc is called Bison.

Usually, a bottom-up parser is going to return an AST representing a successfully parsed source program. The parser generator is given a grammar and runs once to build the parser. The generated parser runs each time a source program is parsed.

Now assume we are parsing the expression 5 ∗ 4 + 3.

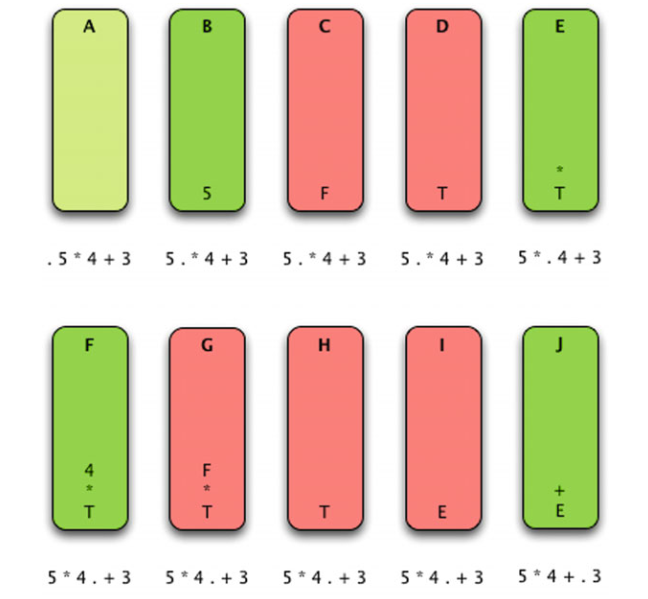
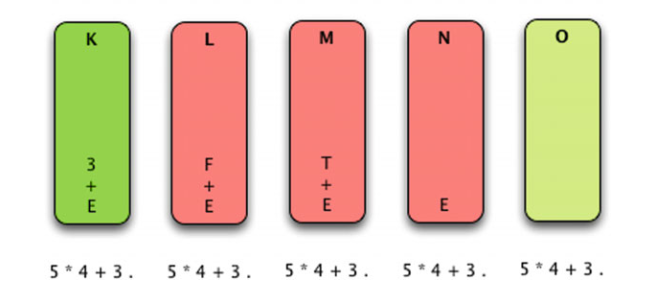
In step O the entire source has been parsed, the stack is empty, and the source program is accepted as a valid program. The actions taken while parsing include shifting and reducing. These are the two main actions of any bottom-up parser. In fact, bottom-up parsers are often called shift-reduce parsers.

2.11 Ambiguity in Grammars

A grammar is ambiguous if there exists more than one parse tree for a given sentence of the language. A classic example of ambiguity in languages arises from nested if-then-else statements.

Consider the following Pascal statement:

if a<b then
    if b<c then
        writeln("a<c")
else
    writeln("?")

The BNF for an if-then-else statement might look something like this.
<statement>::= if <expression> then <statement> else <statement>
$\qquad\qquad$| if <expression> then <statement>
$\qquad\qquad$| writeln (<expression>)

The recursive nature of this rule means that if-then-else statements can be arbitrarily nested. It is unclear if the else goes with the first or second if statement.

When a bottom-up parser is generated using this grammar, the parser generator will detect that there is an ambiguity in the grammar. The first rule says when looking at an else keyword the parser should shift. The second rule says when the parser is looking at an else it should reduce. To resolve this conflict there is generally a way to specify whether the generated parser should shift or reduce. The default action is usually to shift and that is what makes the most sense in this case. By shifting, the else would go with the nearest if statement.