设$X$为非空集合, $2^X$为$X$的幂集.
定义 设$\empty\neq\mathscr{A}\subset2^X$, 若有:
(1)$\empty,X\in \mathscr A$
(2)$\forall A,B \in \mathscr A \rArr A \cup B \in \mathscr A$
(3)$\forall A \in \mathscr A \rArr A^c=X \backslash A \in \mathscr A$
则称$\mathscr A$为$X$上的代数.
定义 称$\mathscr M$为$2^X$上的$\sigma$-代数, 若$\forall \{A_n\}_{n\in\N}\subset\mathscr M$有$\displaystyle\bigcup_{n=1}^{\infty}{A_n}\in\mathscr M$.
定义 设$\mathscr A$是$X$子集上的代数, 设$\mu:\mathscr{A}\rarr[0,+\infty],A \mapsto \mu(A)$且$\mu(\emptyset)=0$.
(1) 若对$\forall A_1,\cdots,A_n\in\mathscr A,A_i\cap A_j=\empty(i\neq j)$有$\mu(\displaystyle\bigcup_{k=1}^n A_k)=\displaystyle\sum_{k=1}^n\mu(A_k)$, 称$\mu$是可加的.
(2) 若对$\mathscr A$上的任意不相交集列$\{A_n\}$有$\displaystyle\bigcup_{k=1}^\infty A_k \in\mathscr A$且$\mu(\displaystyle\bigcup_{k=1}^\infty A_k)=\displaystyle\sum_{k=1}^\infty\mu(A_k)$, 称$\mu$是$\sigma$-可加的.
(3) 若$\mu(X)<+\infty$, 称$\mu$是有限的.
(4) 若$\exists\{A_n\}_{n\in\N}\subset\mathscr A\space s.t.\space X=\displaystyle\bigcup_{n=1}^\infty A_n$且对$\forall n \in \N,\mu(A_n)<+\infty$, 称$\mu$是$\sigma$-有限的.
定义 设$\mathscr M$为$X$的子集上的$\sigma$-代数, 称$(X,\mathscr M)$为可测空间. 设$\mu:\mathscr{M}\rarr[0,+\infty]$且$\sigma$-可加, 称$\mu$为$(X,\mathscr M)$上的测度, 称$(X,\mathscr M,\mu)$为测度空间.
例. Lebsgue测度.
例. $A \subset \displaystyle\bigcup_{k=1}^\infty I_k\subset\R^n, I_k=[a_1^{(k)},b_1^{(k)}]\times\cdots\times[a_n^{(k)},b_n^{(k)}],m(I_k)=\prod_{i=1}^n(b_i-a_i)$, 定义外测度$\mu^*(A)=\inf\{\displaystyle\sum_{k=1}^\infty m(I_k):\displaystyle\bigcup_{k=1}^\infty I_k\supe A\}$.
定义 设$f$为实值函数, $\forall a\in\R$若$\{x\in X:f(x)>a\}$可测, 则称$f$可测. 复值函数可测当且仅当实部与虚部都可测.
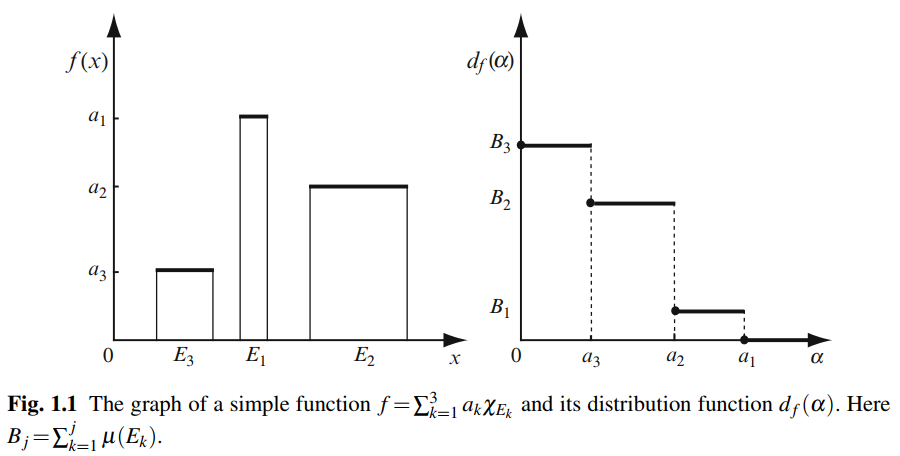
定义 设$f(x)=\displaystyle\sum_{i=1}^k a_i\Large\chi_{E_i}(x)$, $a_i$为常数, $\Large\chi_{E_i}(x)=\begin{cases}1,\quad x\in E_i\\0,\quad x\notin E_i\end{cases},\forall i=1,\cdots,k$.且$E_i\subset X$为$\mu$-可测集, 称$f(x)$为简单函数, 显然$f$为$\mu$-可测函数.
定义 同上一个定义, 定义$\int_X f(x)d\mu=\displaystyle\sum_{k=1}^k a_i\mu(E_i)$
任意可测函数可用简单函数来逼近(详细见实变).
定义 设$f$为$\mu$-可测函数, 设$f^+(x)=\begin{cases}f(x) &f(x)\geqslant0\\0 &f(x)<0\end{cases},f^-(x)=\begin{cases}0 &f(x)\geqslant0\\-f(x) &f(x)<0\end{cases}$, 则$f(x)=f^+(x)-f^-(x),|f(x)|=f^+(x)+f^-(x)$, 若$f$为$\mu$-可积, 则$f^+,f^-$为$\mu$-可积即$\int_X f^+(x)dx<+\infty,\int_X f^-(x)dx<+\infty$, 且$f$可积$\lrArr|f|$可积.
定义 对$0<p<\infty$, 定义$L^p(X,\mu)=\lbrace f:f$为$X$上复值$\mu$-可测函数且$\int_X|f|^pd\mu<\infty\rbrace$, 定义范数$\Vert f\Vert_{L^p(X,\mu)}=(\int_X|f|^pd\mu)^\frac1p$
$\qquad$对$f\in L^\infty(X,\mu)$则$\exists B>0;s.t.;\mu(\{x\in X:|f(x)|>B\})=0$, $\Vert f\Vert_{L^\infty(X,\mu)}=ess.sup|f|=\inf\{B>0:\mu(\{x\in X:|f(x)|>B\})=0\}<+\infty$
例. $X=\R^n,\mu=dx,1\leqslant p<\infty,L^p(\R^n,dx)\overset{def}{=}\lbrace f$为$\R^n$上可测函数$:\int_{\R^n}|f|^pdx<+\infty\rbrace$, $\Vert f \Vert_{L^p(\R^n,dx)}\overset{def}{=}(\int_{R_n}|f(x)|^pdx)^\frac1p$
验证$\Vert\cdot\Vert_{L^p(\R^n,dx)}$是范数.
$1^\circ~\Vert f\Vert_{L^p}\geqslant0$且$\Vert f\Vert_{L^p}=0\lrArr f=0~a.e.~\R^n$.
(注: $f(x)=0~a.e.~\R^n\lrArr\exists Z\subset\R^n,\mu(Z)=0$且$\forall x\in\R^n\backslash Z,f(x)=0$.设$f,g$可测,$f=g\lrArr f=g~a.e.~\R^n$)
$2^\circ~\Vert kf\Vert_{L^p}=|k|\Vert f\Vert_{L^p}(k\in\R)$
$3^\circ(Minkovski$不等式$)$ $\forall f,g\in L^p,\Vert f+g\Vert_{L^p}\leqslant\Vert f\Vert_{L^p}+\Vert g\Vert_{L^p}$
对于$1\leqslant p\leqslant\infty$, $(L^p(X,\mu),\Vert\cdot\Vert_{L^p})$为Banach空间.
定义 若$p,p'>1$且$\frac1p+\frac1{p'}=1$, 则称$p,p'$为共轭指标, $p'=\frac p{p-1}$.
(1) Hölder不等式. 设$p,p',f\in L^p,g\in L^{p'}$则$|\int_X fgd\mu|\leqslant\Vert f\Vert_{L^p}\Vert g\Vert_{L^{p'}}$
(2) $L^p$上的插值不等式. 设$1\leqslant p<q<\infty,f\in L^p\cap L^q$, 则对$\forall p<r<q$有$f\in L^r$且$\Vert f\Vert_{L^r}\leqslant\Vert f\Vert^\theta_{L^p}\cdot\Vert f\Vert^{1-\theta}_{L^q}(\theta\in(0,1),\frac1r=\frac\theta p+\frac{1-\theta}q)$
$\forall 1\leqslant p<\infty$, 有$\Vert f\Vert_{L^p}=\displaystyle\sup_{\Vert g\Vert_{L^{p'}}=1}|\int_X fg~d\mu|$
$p=\infty, X~\sigma$-有限, $\Vert f\Vert_{L^\infty}=\displaystyle\sup_{\Vert g\Vert_{L=1}}|\int_X fg~d\mu|$
设$(L^p)^*$为$L^p$的对偶空间, 则$(L^p)^*\cong L^{p'}, (L^p)^*=L^{p'}$. $1=p$则$L^\infty=(L^1)^*$但$p=\infty,(L^\infty)^*\neq L^1$, $((L^p)^*)^*=L^p$.
设$(X,\mu)$为测度空间. $\empty\subset A\subset X,0=\mu(\empty)\leqslant\mu(A)\leqslant\mu(X=1)$, 称$\mu$为概率测度.
定义 设$f$为$X$上的可测函数, 定义$f$的分布函数$d_f:[0,+\infty)\rarr[0,+\infty],\alpha\mapsto d_f(\alpha)$如下: $$d_f(\alpha)=\mu(E_f(\alpha))=\mu(\{x\in X:|f(x)|>\alpha\})$$
例. 
$d_f(\alpha)=\displaystyle\sum_{j=1}^N B_j\chi_{[\alpha_{j+1},\alpha_j]}(\alpha)$
性质 设$f,g$为$(X,\mu)$上的可测函数, 对$\forall \alpha,\beta>0$有:
(1) $|g|\leqslant|f|~\mu-a.e.\rArr d_g\leqslant d_f$
证明: 设$E_f(\alpha)=\{x\in X:|f(x)|>\alpha\},E_g(\alpha)=\{x\in X:|g(x)|>\alpha\}.$
$|g|\leqslant|f|~\mu-a.e.\rArr\exists Z\subset X,\mu(Z)=0$且$\forall x\in X\backslash Z,|g(x)|\leqslant|f(x)|$.
注意到$E_g(\alpha)=(E_g(\alpha)\backslash Z)\cup(E_g(\alpha)\cap Z)$.
对$\forall x\in E_g(\alpha)\backslash Z$, 有$\alpha<|g(x)|\leqslant|f(x)|\rArr|f(x)|>\alpha\rArr x\in E_f(\alpha)$.
故$E_g(\alpha)\backslash Z\subset E_f(\alpha),(E_g(\alpha)\backslash Z)\cup(E_g(\alpha)\cap Z)\subset E_f(\alpha)\cup(E_g(\alpha)\cap Z)$
从而$d_g(\alpha)=\mu(E_g(\alpha))\leqslant\mu(E_f(\alpha))+\mu(E_g(\alpha)\cap Z)\leqslant\mu(E_f(\alpha))+0=d_f(\alpha)$.
(2) $d_{cf}(\alpha)=d_f(\frac\alpha{|c|}),\forall c\in\mathbb C\backslash\{0\}$.
证明: $E_{cf}(\alpha)=\{x\in X:|cf(x)|>\alpha\}=\{x\in X:|f(x)|>\frac\alpha{|c|}\}=E_f(\frac\alpha{|c|})$.
(3) $d_{f+g}(\alpha+\beta)\leqslant d_f(\alpha)+d_g(\beta)$
证明: $\forall x\in E_{f+g}(\alpha+\beta),|f(x)|+|g(x)|\geqslant|f(x)+g(x)|>\alpha+\beta$. 即若$x\in E_{f+g}(\alpha+\beta)$则$|f(x)|>\alpha$或者$|g(x)|>\beta$故$x\in E_f(\alpha)\cup E_g(\beta)$即$E_{f+g}(\alpha+\beta)\subseteq E_f(\alpha)\cup E_g(\beta)$. 故$\mu(E_{f+g}(\alpha+\beta))\leqslant\mu(E_f(\alpha))+\mu(E_g(\beta))\rArr d_{f+g}(\alpha+\beta)\leqslant d_f(\alpha)+d_g(\beta)$.
推论 $d_{f+g}(\alpha)\leqslant d_f(\frac\alpha2)+d_g(\frac\alpha2)=d_{2f}(\alpha)+d_{2g}(\alpha)$.
(4) $d_{fg}(\alpha\beta)\leqslant d_f(\alpha)+d_g(\beta)$ (由$E_{fg}(\alpha\beta)\subseteq E_f(\alpha)\cup E_g(\beta)$).
(5) $d_f(\alpha)$单调递减.
$\forall \alpha_1<\alpha_2,\mu(E_f(\alpha_1))\geqslant\mu(E_f(\alpha_2))$
(6) $d_f(\alpha)$在$\alpha_i$右连续.
设$\alpha_n\rarr\alpha(n\rarr\infty)$递减$d_f(\alpha)=\mu(E_f(\alpha))=\mu(\displaystyle\bigcup_{n=1}^\infty E_f(\alpha_n))=\mu(\lim_{n\rarr\infty}E_f(\alpha_n))=\lim_{n\rarr\infty}\mu(E_f(\alpha_n))=\lim_{n\rarr\infty}d_f(\alpha_n)$.
(7) 设可测函数列$\{f_n\}:0\leqslant f_1\leqslant f_2\leqslant\cdots\rarr f~(n\rarr\infty)a.e.~x\in X\rArr d_{f1}(\alpha)\leqslant\cdots\leqslant d_{f_n}(\alpha)\leqslant\cdots(n\rarr\infty)\rarr d_f(\alpha)$.
$\begin{aligned}(8)\forall 1\leqslant p<\infty,d_f(\alpha)&\leqslant\alpha^{-p}\int_{E_f(\alpha)}|f(x)|^pdx\\&=\alpha^{-p}\int_{|f(x)|>\alpha}|f(x)|^pdx\\&\leqslant\alpha^{-p}\int_X|f(x)|^pdx\end{aligned}$
证明: $$ \begin{aligned} d_f(\alpha)=\mu(E_f(\alpha))&=\mu(\{x\in X:|f(x)|>\alpha\})\\ &=\mu(\{x\in X:(\frac{|f(x)|}\alpha)^p>1\})\\ &=\int_{E_f(\alpha)}1dx=\int_X \chi_{E_f(\alpha)}(x)dx\\ &\leqslant\int_{E_f(\alpha)}\frac{|f(x)|^p}{\alpha^p}dx=\alpha^{-p}\int_{E_f(\alpha)}|f(x)|^pdx \end{aligned} $$
Fubini定理 设$(X_1,\mathscr{M}_1,\mu_1),(X_2,\mathscr{M}_2,\mu_2)$为完备的$\sigma$-有限的测度空间, $f(x_1,x_2)$为$(X_1\times X_2,\mu_1\times\mu_2)$上的可测函数, 则
(1) 对几乎所有$x_2\in X_2,f^{x_2}(x_1)=f(x_1,x_2)$在$(X_1,\mu_1)$上可积.
(2) $\int_{X_1}f(x_1,x_2)d\mu_1$为$X_2$上可积函数.
(3) $\int_{X_2}(\int_{X_1}f(x_1,x_2)d\mu_1)d\mu_2=\int_{X_1\times X_2}fd\mu_1\times\mu_2$.
引理 设$1\leqslant p<\infty,f\in L^p(X,\mu)$, 则$\alpha^{p-1}d_f(\alpha)\in L^1([0,+\infty))$且$p\int_0^{+\infty}\alpha^{p-1}d_f(\alpha)d\alpha=\int_X|f(x)|^pd\mu=\Vert f\Vert^p_{L^p}$
证明: $$ \begin{aligned} &p\int_0^{+\infty}\alpha^{p-1}d_f(\alpha)d\alpha\\&=p\int_0^{+\infty}\alpha^{p-1}\mu(E_f(\alpha))d\alpha\\ &=p\int_0^{+\infty}\alpha^{p-1}(\int_{\{x:|f(x)|>\alpha\}}1d\mu)d\alpha\\ &=p\int_0^{+\infty}\alpha^{p-1}\int_X \chi_{E_f(\alpha)}d\mu d\alpha \end{aligned} $$ 注意到$\{(\alpha,X):0\leqslant\alpha<\infty,|f(x)|>\alpha\}=\{(\alpha,x):x\in X,0\leqslant\alpha<|f(x)|\}$, 由Fubini定理,$$ \begin{aligned} &p\int_0^{+\infty}\alpha^{p-1}d_f(\alpha)d\alpha\\&=p\int_0^{+\infty}\alpha^{p-1}\int_X \chi_{E_f(\alpha)}d\mu d\alpha\\&=p\int_{\{(\alpha,x):x\in X,0\leqslant\alpha<|f(x)|\}}\alpha^{p-1}\cdot1d\alpha d\mu\\&=\int_X\int_0^{|f(x)|}p\alpha^{p-1}d\alpha d\mu\\&=\int_X(\alpha^p|^{f(x)}_0)d\mu=\int_X|f(x)|^pd\mu \end{aligned} $$
性质 $f\in L^p(X,\mu)(1\leqslant1<\infty)$, 则$\lim\limits_{\alpha\rarr+\infty}\alpha^pd_f(\alpha)=\lim\limits_{\alpha\rarr0^+}\alpha^pd_f(\alpha)=0$
证明: 由引理,$\int_0^{+\infty}t^{p-1}d_f(t)dt=\frac1p\Vert f\Vert^p_{L^p}<+\infty$. 设$I_1(\alpha)\equiv\int_{\frac\alpha2}^\alpha t^{p-1}d_f(t)dt$, 由$d_f$递减, $I_1(\alpha)\geqslant d_f(\alpha)\int_{\frac\alpha2}^\alpha t^{p-1}dt=d_f(\alpha)\frac1p(\alpha^p-(\frac\alpha2)^p)=\alpha^p d_f(\alpha)\cdot\frac1p(1-2^{-p})$
故$0\leqslant\alpha^p d_f(\alpha)\leqslant\frac{p}{1-2^{-p}}\int_{\frac\alpha2}^\alpha t^{p-1}d_f(t)dt\rarr0(\alpha\rarr0^+,\alpha\rarr+\infty)$
注: $1^\circ~d_f(\alpha)=o(\alpha^{-p})(\alpha\rarr0^+,\alpha\rarr+\infty)$
$2^\circ~1\leqslant p<\infty,\alpha>0$给定, $f(x)=f(x)1_{\lbrace x:|f(x)|>\alpha\rbrace}+f(x)1_{\lbrace x:|f(x)|\leqslant\alpha\rbrace}=b(x)+g(x)$ (bad part, good part)
($~\int_X1_{\lbrace x:|f(x)|>\alpha\rbrace}d\mu=\int_X1_{E_f(\alpha)}(x)d\mu=d_f(\alpha)~$)
(1)$f\in L^p(X,\mu)\rArr\forall r<p,b(x)\in L^r(X,\mu)$
事实上, $\int_X|b(x)|^rd\mu=\int_X|f(x)|^r1_{E_f(\alpha)}(x)d\mu=\int_{|f(x)|>\alpha}|f(x)|^rd\mu=\int_{|f(x)|>\alpha}|f(x)|^p|f(x)|^{r-p}d\mu\leqslant\int_{|f(x)|>\alpha}|f(x)|^pd\mu\cdot\alpha^{p-r}\leqslant\int_X|f(x)|^pd\mu\cdot\alpha^{p-r}<\infty\rArr b\in L^r(X,\mu)$
(2) $\forall q\geqslant p,g(x)\in L^q(X,\mu)$. 同理可证.
$\int_X|f|^pd\mu=p\int_0^{+\infty}\alpha^{p-1}d_f(\alpha)d\alpha=p\int_0^{+\infty}[\alpha\cdot d_f^{\frac1p}(\alpha)]^p\frac{d\alpha}\alpha\rArr\alpha d_f^{\frac1p}(\alpha)\in L^p([0,+\infty),\frac{d\alpha}\alpha])$.